Профессиональному электрику, специалисту электронщику никак не обойти в собственной деятельности закон Ома, решая любые задачи, связанные с наладкой, настройкой, ремонтом электронных и электрических схем.
Собственно, понимание этого закона необходимо каждому. Потому что каждому в быту приходится иметь дело с электричеством.
И хотя учебным курсом средней школы закон немецкого физика Ома и предусмотрен, но на практике не всегда своевременно изучается. Поэтому рассмотрим в нашем материале такую актуальную для жизни тему и разберемся с вариантами записи формулы.
Отдельный участок и полная электрическая цепь
Рассматривая электрическую цепь с точки зрения применения к схеме закона Ома, следует отметить два возможных варианта расчета: для отдельно взятого участка и для полноценной схемы.
Расчет тока участка электрической схемы
Участком электрической цепи, как правило, рассматривается часть схемы, исключающая источник ЭДС, как обладающий дополнительным внутренним сопротивлением.
Поэтому расчетная формула, в данном случае, выглядит просто:
I = U/ R,
Трактовка формулы простая – ток, протекающий по некоему участок цепи, пропорционален приложенному к нему напряжению, а сопротивлению – обратно пропорционален.
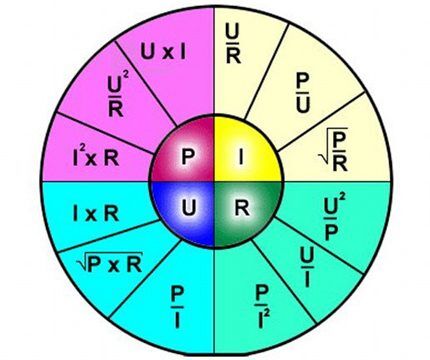
Так называемая графическая «ромашка», посредством которой представлен весь набор вариаций формулировок, основанных на законе Ома. Удобный инструмент для карманного хранения: сектор «P» — формулы мощности; сектор «U» — формулы напряжения; сектор «I» — формулы тока; сектор «R» — формулы сопротивления
Таким образом, формулой чётко описывается зависимость протекания тока по отдельному участку электрической цепи относительно определенных значений напряжения и сопротивления.
Формулой удобно пользоваться, например, рассчитывая параметры сопротивления, которое требуется впаять в схему, если заданы напряжение с током.
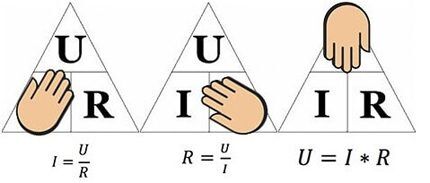
Закон Ома и два следствия, которыми необходимо владеть каждому профессиональному электромеханику, инженеру-электрику, электронщику и всем, кто связан с работой электрических цепей. Слева направо: 1 — определение тока; 2 — определение сопротивления; 3 — определение напряжения, где I — сила тока, U — напряжение, R — сопротивление
Вышеприведенный рисунок поможет определить, например ток, протекающий через 10-омное сопротивление, к которому приложено напряжение 12 вольт. Подставив значения, найдем – I = 12 / 10 = 1.2 ампера.
Аналогично решаются задачи поиска сопротивления (когда известны ток с напряжением) или напряжения (когда известны напряжение с током).
Физика 10 класс (Урок№31 — Закон Ома для полной цепи.)
Тем самым всегда можно подобрать требуемое рабочее напряжение, нужную силу тока и оптимальный резистивный элемент.
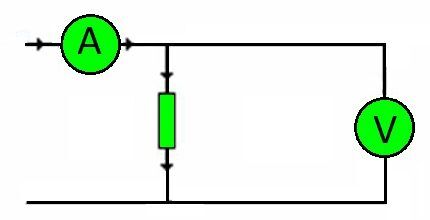
Формула, которой предложено пользоваться, не требует учитывать параметры источника напряжения. Однако, схема, содержащая, например, аккумулятор, будет рассчитываться по другой формуле. На схеме: А – включение амперметра; V – включение вольтметра.
Кстати, соединительные провода любой схемы – это сопротивления. Величина нагрузки, которую им предстоит нести, определяется напряжением.
Соответственно, опять же пользуясь законом Ома, становится допустимым точный подбор необходимого сечения проводника, в зависимости от материала жилы.
У нас на сайте есть подробная инструкция по расчету сечения кабеля по мощности и току.
Вариант расчета для полной цепи
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС.
Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС.
Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
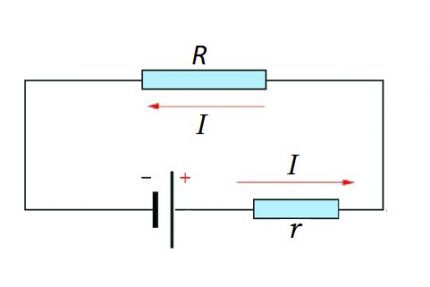
Для расчетов в условиях полноценной электрической цепи всегда берется к учету резистивное значение источника ЭДС. Это значение суммируется с резистивным сопротивлением непосредственно электрической цепи. На схеме: I — прохождение тока; R — резистивный элемент внешний; r — резистивный фактор ЭДС (источника энергии)
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины.
Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Рассмотрение действия закона к переменной величине
Понятие «сопротивление» к условиям прохождения переменного тока следует рассматривать уже больше как понятие «импеданса». Здесь имеется в виду сочетание активной резистивной нагрузки (Ra) и нагрузки, образованной реактивным резистором (Rr).
Обусловлены подобные явления параметрами индуктивных элементов и законами коммутации применительно к переменной величине напряжения — синусоидальной величине тока.

Такой видится эквивалентная схема электрической цепи переменного тока под расчет с применением формулировок, исходящих из принципов закона Ома: R — резистивная составляющая; С — емкостная составляющая; L — индуктивная составляющая; ЭДС -источник энергии; I -прохождение тока
Другими словами, имеет место эффект опережения (отставания) токовых значений от значений напряжения, что сопровождается появлением активной (резистивной) и реактивной (индуктивной или емкостной) мощностей.
Расчёт подобных явлений ведётся при помощи формулы:
Z = U / I или Z = R + J * (XL — XC)
где: Z – импеданс; R – активная нагрузка; XL , XC – индуктивная и емкостная нагрузка; J – коэффициент.
Закон Ома для полной цепи
Закон Ома для полной цепи – эмпирический (полученный из эксперимента) закон, который устанавливает связь между силой тока, электродвижущей силой (ЭДС) и внешним и внутренним сопротивлением в цепи.
При проведении реальных исследований электрических характеристик цепей с постоянным током необходимо учитывать сопротивление самого источника тока. Таким образом в физике осуществляется переход от идеального источника тока к реальному источнику тока, у которого есть свое сопротивление (см. рис. 1).

Рис. 1. Изображение идеального и реального источников тока
Рассмотрение источника тока с собственным сопротивлением обязывает использовать закон Ома для полной цепи.
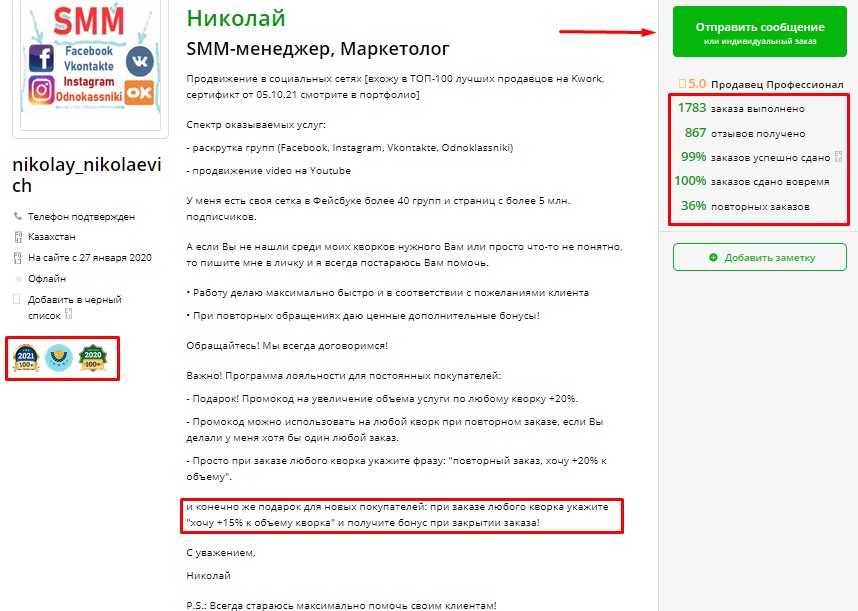
Сформулируем закона Ома для полной цепи так (см. рис. 2): сила тока в полной цепи прямо пропорциональна ЭДС и обратно пропорциональна полному сопротивлению цепи, где под полным сопротивлением понимается сумма внешних и внутренних сопротивлений.

Рис. 2. Схема закона Ома для полной цепи.
Формула закона Ома для полной цепи

- R – внешнее сопротивление [Ом];
- r – сопротивление источника ЭДС (внутреннее) [Ом];
- I – сила тока [А];
- ε– ЭДС источника тока [В].
Рассмотрим некоторые задачи на данную тему. Задачи на закон Ома для полной цепи, как правило, дают ученикам 10 класса, чтобы они могли лучше усвоить указанную тему.
I. Определите силу тока в цепи с лампочкой, сопротивлением 2,4 Ом и источником тока, ЭДС которого равно 10 В, а внутреннее сопротивление 0,1 Ом.
По определению закона Ома для полной цепи, сила тока равна:

II. Определить внутреннее сопротивление источника тока с ЭДС 52 В. Если известно, что при подключении этого источника тока к цепи с сопротивлением 10 Ом амперметр показывает значение 5 А.
Запишем закон Ома для полной цепи и выразим из него внутреннее сопротивление:

III. Однажды школьник спросил у учителя по физике: «Почему батарейка садится?» Как грамотно ответить на данный вопрос?
Мы уже знаем, что реальный источник обладает собственным сопротивлением, которое обусловлено либо сопротивлением растворов электролитов для гальванических элементов и аккумуляторов, либо сопротивлением проводников для генераторов. Согласно закону Ома для полной цепи:

следовательно, ток в цепи может уменьшаться либо из-за уменьшения ЭДС, либо из-за повышения внутреннего сопротивления. Значение ЭДС у аккумулятора почти постоянный. Следовательно, ток в цепи понижается за счет повышения внутреннего сопротивления. Итак, «батарейка» садится, так как её внутреннее сопротивление увеличивается.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.
Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.
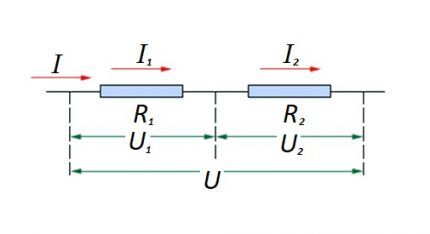
Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U, U1, U2 — приложенное напряжение
Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.
Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
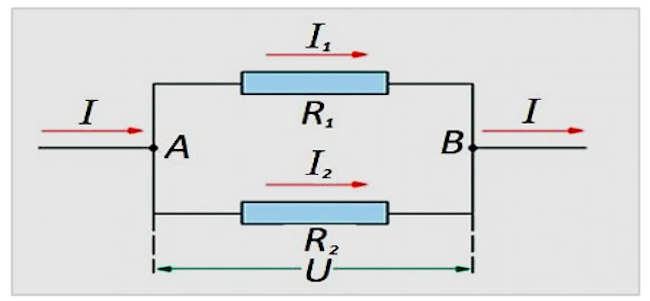
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.
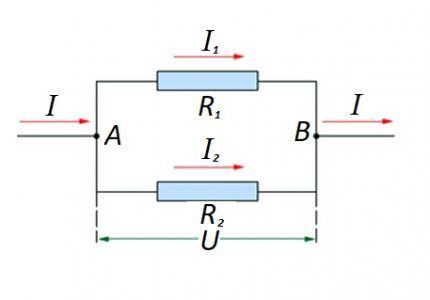
Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U — подведённое напряжение; А, В — точки входа/выхода
Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.
Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E
Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ
Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Выводы и полезноеМнемоническая диаграмма
Для лучшего запоминания закона Ома существует мнемоническая диаграмма, благодаря которой можно всегда напомнить себе формулу. Пользоваться этой диаграммой очень просто. Достаточно закрыть искомую величину и две другие укажут, как её найти . Потренируйтесь, это может вам пригодится.
Успехов в изучении электричества! Рекомендуем прочесть статью — законы Кирхгофа.
Графическая интерпретация закона Ома
Закон Ома для участка цепи можно проиллюстрировать с помощью так называемого треугольника Ома:

Этот треугольник наглядно демонстрирует связь между током I, напряжением U и сопротивлением R:
- ток I пропорционален напряжению U и обратно пропорционален R;
- если U растёт, то растёт и I;
- если R растёт, то I уменьшается.

Треугольник Ома наглядно демонстрирует качественную зависимость между величинами, о которой говорит закон Ома. Это помогает лучше понять физический смысл закона.
Далее рассмотрим примеры применения закона Ома для расчёта электрических цепей.
Примеры применения закона Ома
Рассмотрим пример использования закона Ома для расчёта электрической цепи постоянного тока. Допустим, цепь состоит из источника с ЭДС E = 50 В с внутренним сопротивлением r = 5 Ом, к которому последовательно подключены резисторы с сопротивлениями R1 = 10 Ом, R2 = 20 Ом и R3 = 15 Ом. Требуется найти силу тока в цепи.
Согласно закону Ома, сила тока рассчитывается по формуле:
Полное сопротивление цепи равно:
R = r + R1 + R2 + R3 = 5 + 10 + 20 + 15 = 50 Ом.
Подставляя числовые значения в формулу закона Ома, получаем:
I = 50 В / 50 Ом = 1 А.
Таким образом, сила тока в данной цепи постоянного тока равна 1 А.
Рассмотрим ещё один пример, где резисторы соединены параллельно. Пусть цепь состоит из источника напряжением U = 100 В и двух параллельно соединённых резисторов с сопротивлениями R1 = 10 Ом и R2 = 20 Ом.
Полное сопротивление при параллельном соединении вычисляется по формуле:
R = (R1 * R2) / (R1 + R2) = (10 * 20) / (10 + 20) = 6,67 Ом.
По закону Ома сила тока в цепи:
I = U / R = 100 В / 6,67 Ом = 15 А.
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).
Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=frac
- varepsilon — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.

.

- U — электрическое напряжение;
- I — сила тока;
- P — электрическая мощность;
- R — электрическое сопротивление
Смотри также:
- Первый закон Ньютона
- Второй закон Ньютона
- Третий закон Ньютона
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
Последовательное и параллельное включение элементов
Элементы полной цепи или участка цепи могут соединяться последовательно или параллельно. Для каждого варианта действие тока и напряжения будет разным, поэтому закон Ома для замкнутой цепи в обоих случаях тоже отличается. Данный физические свойства комбинированно используются в различных электрических схемах.
Формула для закона Ома
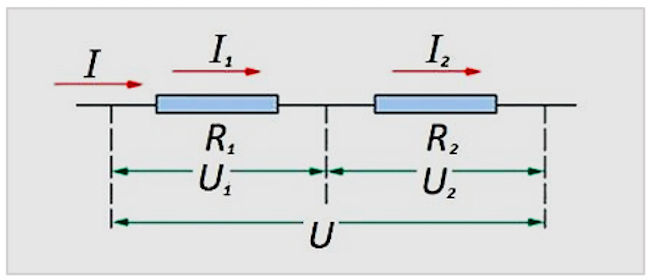
Цепь последовательно включенных резистивных элементов
Если в качестве примера взять два элемента на отдельном участке, то поведение основных величин можно записать в следующем виде:
- I = I1= I2 (силы токов равны)
- U = U1+ U2 (общее напряжение состоит из суммы напряжений)
- R = R1+ R2 (общее сопротивление также является суммой двух сопротивлений)
Отсюда можно сделать вывод, что вне зависимости от количества резистивных элементов 1, 2 или 3, соединенных последовательно, сила тока на участке остается неизменной. Общее значение напряжения эквивалентно источнику ЭДС, а для каждого компонента определяется основной формулой закона Ома.
Цепь параллельно включенных резистивных элементов
При параллельном подключении действие закона Ома происходит несколько иначе:
- I = I1+ I2 … (силы токов, проходящих через элементы, складываются)
- U = U1= U2 … (все напряжения равны между собой)
- 1 / R = 1 / R1+ 1 / R2 + … (сопротивление суммируется по отдельной схеме)
Довольно часто используются смешанные схемы подключения, в которых используются оба варианта, объединенные в замкнутый контур. В этом случае сначала рассчитывается общий резистивный номинал на участке с параллельным подключением, после чего к полученному результату добавляется значение резистора на последовательном соединении.
Интегральная и дифференциальная формы закона
Все варианты, рассмотренные выше, подходят ближе к идеальным условиям, где каждый элемент имеет свой постоянный показатель. В том числе и в проводниках рассматривается однородная структура, хотя на практике такое встречается очень редко. Большинство схем состоят из множества участков, на которых используются разные проводники, отличающиеся материалом и сечением.
Интегральная форма расчетов практически совпадает с действием закона Ома для полной цепи и других его производных. Следовательно, сила тока, протекающего в проводнике, будет зависеть от разности потенциалов на его концах и его полного сопротивления. То есть, напряжение можно определить: I * R = φ1 – φ2 + έ или же U=I x R.
Скин-эффект. Принцип работы
Дифференциальная форма используется в основном для изучения и теоретических расчетов бесконечно малых проводников на ничтожно малом участке цепи. Коротко это можно написать в таком виде:
В этом выражении А является удельной теплопроводностью, E – напряженностью электрического поля, j – плотностью потока частиц с электрическим зарядом. Следовательно, произведение ej будет плотностью электрического тока. Поскольку Закон Ома в данном случае касается лишь одной точки, поэтому он и получил название дифференциальной формы.
Выводы
В данной статье мы постарались дать простое объяснение закона Ома для полной цепи. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Специалисты в области электрики и электроники в своей работе постоянно используют закон Ома для полной электрической цепи и ее отдельных участков.

Закон Ома для переменного тока

Как понять Закон Ома: простое объяснение для чайников с формулой и понятиями
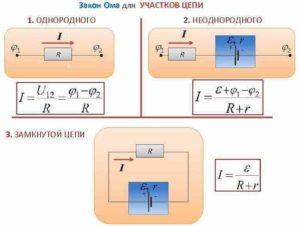
Закон Ома для однородного участка цепи – формула
Закон Ома для полной и не полной электрической цепи, формула и правильное определение
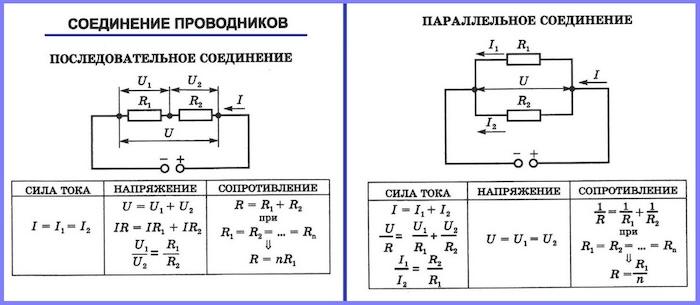
Ток и напряжение при параллельном, последовательном и смешанном соединении проводников

Мультиметр: назначение, виды, обозначение, маркировка, что можно измерить мультиметром




