Фильтр низких частот это

Фильтр нижних частот является схемой, которая без изменений передает сигналы нижних частот, а на высоких частотах обеспечивает затухание сигналов и за­паздывание их по фазе относительно входных сигналов.

Пассивные фильтры нижних частот первого порядка

На рис.2.25 изображена схема простого RС-фильтра нижних ча­стот первого порядка. Коэффициент передачи в комплексном виде может быть выражен формулой:

. (2.45)
Рис. 2.25 Отсюда получим формулы для АЧХ и ФЧХ

Положив получим выражение для частоты среза ωСР

Фазовый сдвиг на этой частоте составляет – 450 .
| К | = 1 = 0 дБ на нижних частотах f fCР .
На высоких частотах f >> fСР согласно формуле (2.46), | К | ≈ 1/ (ωRC),
т.е. коэффи­циент передачи обратно пропорционален частоте. При увеличении частоты в 10 раз коэффициент усиления уменьшается в 10 раз, т. е. он уменьшается на 20 дБ на дека­ду или на 6 дБ на октаву. | К | = 1/√2 = -ЗдБ при f = fСР .
Для более быстрого уменьшения коэффициента передачи можно включить n фильтров нижних частот последовательно. При последовательном соединении нескольких фильтров нижних частот частота среза приближенно определяется как

Для случая n фильтров с равными частотами среза

При частоте входного сигнала fВХ>> fСР для схемы (рис. 2.25) получим

Из 2.50 видно, что ФНЧ может выступать как интегрирующее звено.
Для переменного напряжения, содержащего постоянную составляющую выходное напряжение можно представить в виде

где — среднее значение
Фильтр нижних частот может выступать в качестве детектора средних значений.
Для реализации общего подхода к описанию фильтров необходимо нормировать комплексную переменную р.

Для фильтра рис. 2.25 получим Р = рRC и

Использую передаточную функцию для оценки амплитуды выходного сигнала от частоты, получим

Передаточная функция ФНЧ в общем виде может быть записана в виде

где с1, с2 ,…, сn– положительные действительные коэффициенты.
Порядок фильтра определяется максимальной степенью переменной Р. Для реализации фильтра необходимо разложить полином знаменателя на множители. Если среди корней полинома есть комплексные, в этом случае следует записать полином в виде произведения сомножителей второго порядка

где аi и bi– положительные действительные коэффициенты. Для нечетных порядков полинома коэффициент b1 равен нулю.

Активные фильтры нижних частот первого порядка

Простой фильтр, изображенный на рис. 2.26, обладает недостатком: свойства фильтра зависят от нагрузки. Для устранения этого недостатка фильтр необходимо дополнить преобразователем полного сопротивления. Схема фильтра с преобразователем полного сопротивления показана на рис. 2.27. Коэффициент передачи постоянного сигнала может быть задан выбором значений резисторов R2 и R3.

ВЧ-фильтры. Часть 2. ФНЧ ФВЧ. Начинающим радиоконструкторам. Ликбез.

Для упрощения схемы ФНЧ можно использовать RC- цепь для обратной связи операционного усилителя. Подобный фильтр показан на рис. 2.27.

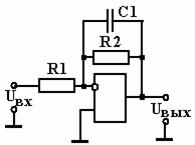
Передаточная функция фильтра (рис. 2.27) имеет вид

Для расчета фильтра необходимо задать частоту среза fСР (ωСР), коэффициент передачи постоянного сигнала К0 (для схемы на рис. 2.27 он должен быть задан со знаком минус) и емкость конденсатора С1. Приравняв коэффициенты полученной передаточной функции коэффициентам выражения 2.56 для фильтра первого порядка, получим

Пассивный фильтр нижних частот второго порядка

На основании выражения (2.56) запишем в общем виде передаточную функцию ФНЧ второго порядка

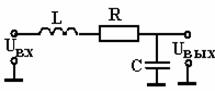
Такая передаточная функция не может быть реализована с помощью пассивных RC-цепей. Подобный фильтр может быть реализован с применением индуктивностей. На рис. 2.28 показана схема пассивного ФНЧ второго порядка.
Передаточная функция фильтра имеет вид
. (2.61)
Рассчитать фильтр можно, воспользовавшись формулами
Рис. 2.28
и . (2.62)
Например, для ФНЧ второго порядка типа Баттерворта с коэффициентами а1 = 1,414 и b1 = 1,000, задав частоту среза fСР= 10 Гц и емкость С = 10мкФ, из (2.62) получим R = 2,25 кОм и L = 25,3 Гн.
Подобные фильтры неудобны для реализации из-за слишком большой индуктивности. Заданную передаточную функцию можно реализовать с помогщью операционного усилителя с соответствующими RC – цепями, что позволяет исключить индуктивности.

Активные ФНЧ второго порядка

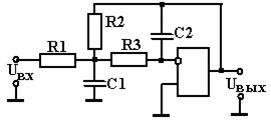
Примером активного ФНЧ второго порядка является фильтр со сложной отрицательной обратной связью, схема которого показана на рис. 2.29.
Передаточная функция данного фильтра имеет вид

Рис. 2.29
Для расчета фильтра можно записать

При расчете схемы лучше задавать значения емкостей конденсаторов и вычислять необходимые значения сопротивлений.

Для того чтобы значение сопротивления R2 было действительным, должно выполняться условие

Фильтры с отрицательной обратной связью могут быть реализованы с высокой добротностью.
Активный ФНЧ второго порядка может быть построен на основе ОУ с омической отрицательной обратной связью и на основе ОУ с положительной обратной связью. Примеры подобных фильтров показаны на рис. 2.30 и рис. 2.31.

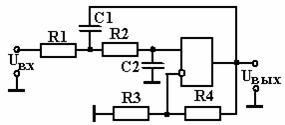
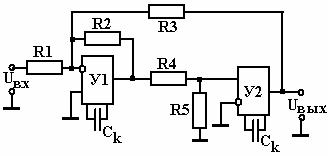
Рис. 2.30 Рис. 2.31

ФНЧ третьего и более высоких порядков

Для реализации ФНЧ более высокого порядка, чем второй, можно последовательно соединить фильтры первого и второго порядка. В этом случае характеристики звеньев фильтра перемножаются. Однако, чтобы результат перемножения частотных характеристик звеньев фильтра соответствовал желаемому типу фильтра, необходимо задавать соответствующие коэффициенты звеньев фильтра. На рис. 2.32 приведен пример реализации ФНЧ Бесселя третьего порядка.

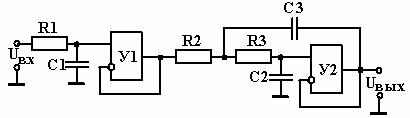
Рис. 2.32

Пусть частота среза фильтра fСР = 100 Гц. Задав значение емкости С1 = 100 нФ, из выражения , получим R1 = 12,03 кОм. Для второго каскада фильтра зададим С3 = 100 нФ. Для второго каскада, чтобы R2 и R3 были действительными должно выполняться условие

Из этого условия находим С2

Выбрав R2 = R3, получим

Выбрав С2 из стандартного ряда С2 = 47 нФ получим
R2 = 11,51 кОм; R3 = 22,33 кОм.
В схеме рис. 2.32 ФНЧ первого порядка может быть выполнен на пассивных элементах (простой RC-фильтр).

Термин: Фильтр низкой частоты

Фильтр низкой частоты (ФНЧ, low-pass filter) – это устройство, подавляющее частоты сигнала выше частоты среза данного фильтра. На рисунке приведена амплитудно-частотная характеристика типичного ФНЧ. Единице условно присвоена максимальная амплитуда сигнала, точка с амплитудой 0,7 (-3 дБ) соответствует частоте среза ФНЧ, относительно которой производится расчёт ФНЧ по большинству существующих методик. От нулевой частоты до частоты среза ФНЧ находится полоса частот пропускания, справа – полоса частот подавления (задержания).

Подавление высокочастотных составляющих частот сигнала приводит к подавлению деталей сигнала с большими скоростями нарастания. ФНЧ всегда сглаживает сигнал, внося собственную задержку фильтра. Постоянную составляющую сигнала ФНЧ всегда пропускает.

ФНЧ традиционно применяют для улучшения сигнал/шум сигнального тракта за счёт подавления помех с частотами выше, чем верхняя граница полосы частот информационного сигнала. ФНЧ также широко применяют для подавления высокочастотных помех в цепях питания и сигнальных цепях в целях обеспечения электромагнитной совместимости аппаратуры.

ФНЧ могут быть как аналоговые, так и цифровые.

Аналоговые ФНЧ бывают активными (требуют дополнительной энергии питания для своей работы) и пассивными (не требуют дополнительной энергии питания). Активный аналоговый ФНЧ использует микроэлектронную технологию (типично: операционные усилители), пассивный аналоговый ФНЧ может быть сделан как на пассивных электронных компонентах (RC-фильтр, RLC-фильтр), так и с использованием пьезоэффекта, кварцевых резонаторов, объёмных резонаторов и прочих физических резонансных принципов.

Цифровые ФНЧ (фильтр цифрового сигнала) – это большое семейство вычислительных алгоритмов ЦОС. Принципиально цифровой фильтр может быть рекурсивным (с обратными связями в своём алгоритме) и нерекурсивным (без обратных связей). Принципиально, что АЧХ цифрового фильтра на частотной оси периодична: в частности, выше половины частоты дискретизации начинается зеркальная АЧХ цифрового фильтра.

Основные характеристики физически реализованного ФНЧ:

• Частота среза.
• Неравномерность в полосе частот пропускания, амплитудно-частотная характеристика (АЧХ).
• Групповая задержка фильтра, фазочастотная характеристика (ФЧХ).
• Динамический диапазон.
• Рабочий диапазон сигнала в полосе частот пропускания.
• Рабочий диапазон сигнала в полосе частот подавления.

На последней характеристике стоит остановиться отдельно, поскольку она довольно коварна. Любой физически реализованный фильтр всегда имеет реальный конечный диапазон сигнала, при котором он способен корректно выполнять свою функцию. При превышении этого диапазона, в зависимости от технологии фильтра, может наступить ограничение, сложное искажение сигнала и прочие нелинейные эффекты. Но на практике данные эффекты легко идентифицировать в полосе пропускания ФНЧ, но довольно тяжело диагностировать в полосе подавления, поскольку значительная часть искаженного сигнала эффективно подавляется, а остальная часть – может вызвать странные эффекты. Таким образом, о непревышении рабочего диапазона сигнала в полосе подавления нужно помнить в реальных условиях применения ФНЧ.

Активный фильтр высоких частот (ФВЧ) первого порядка

Активный ФВЧ 1 порядка формируется на базе схемы инвертирующего усилителя добавлением конденсатора последовательно с входным резистором R1.

Реактивное сопротивление конденсатора обратно пропорционально частот сигнала.

Запишем уравнение первого закона Кирхгофа для узла инвертирующего входа, учитывая гипотезу идеальности ОУ (iвх≈0)

Согласно гипотезе идеальности ОУ U — =U + =0, тогда

Таким образом, коэффициент передачи схемы – комплексное выражение, модуль которого зависит от частоты. Проанализируем поведение модуля и фазы коэффициента передачи в частотной области.

Зависимость модуля коэффициента передачи от частоты, называемая амплитудно-частотной характеристикой (АЧХ), имеет аналитическое выражение:

Зависимость модуля коэффициента передачи в логарифмических единицах — децибелах от частоты в логарифмическом масштабе называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ). Асимптотическая ЛАЧХ представляет собой ломаную линию с изломом в точке, соответствующей частоте среза fср=ωср/2∙π=1/(2∙π∙R2∙C).

Реальная ЛАЧХ отличается от асимптотической, причем максимальное отклонение наблюдается на частоте среза и составляет -3 дБ, что в нормальном масштабе соответствует уменьшению коэффициента передачи в √2 раз. Коэффициент передачи в полосе пропускания составляет 20lg(R2/R1). Наклон ЛАЧХ в полосе задерживания определяется как +20дБ/дек, что поясняется следующими соотношениями.

omegacdot Ccdot R_1 = 0.1 Rightarrow |K_U|=displaystylefraccdotdisplaystylefrac>approx 0.1displaystylefrac .

omegacdot Ccdot R_1 = 0.01 Rightarrow |K_U|=displaystylefraccdotdisplaystylefrac>approx 0.01displaystylefrac .

Таким образом, десятикратное изменение частоты соответствует десятикратному изменению коэффициента усиления.

Работа ФВЧ иллюстрируется моделью в программе LTspice

Работа ФНЧ при различных значениях сопротивления входного резистора иллюстрируется моделью в программе LTspice

В области высоких частот на свойства активного фильтра начинают оказывать влияние свойства примененного операционного усилителя, поэтому наблюдается уменьшение модуля коэффициента передачи.

Работа ФВЧ при различных значениях емкости конденсатора иллюстрируется моделью в программе LTspice

Полосовой фильтр (ПФ) первого порядка

Полосовой фильтр первого порядка можно реализовать на базе схемы инвертирующего усилителя заменой входного резистора на последовательное соединение цепи R1C1, как в ФВЧ, и заменой резистора обратной связи на параллельное соединение цепи R2C2, как в ФНЧ.

Записывая уравнение первого закона Кирхгофа для узла инвертирующего входа, имеем:

Используя гипотезу идеальности ОУ, аналогично ФВЧ и ФНЧ можно записать:

f_1lt f_2Longrightarrow tau_1gttau_2

displaystylefracge 3div 10.

Работа полосового фильтра (ПФ) иллюстрируется моделью в программе LTspice.

Работа ПФ при различных значениях емкости конденсатора во входной цепи иллюстрируется моделью в программе LTspice

Работа ПФ при различных значениях емкости конденсатора в цепи обратной связи иллюстрируется моделью в программе LTspice

Как использовать Low-Pass фильтр при сведении музыки

Самое частое применение фильтра — обрезка высоких частот. Благодаря этому сигнал становится чище, а в верхнем диапазоне частот микса появляется дополнительное пространство для инструментов. Тем не менее возможности низкочастотного фильтра не ограничиваются простой чисткой спектра, ведь фильтр может работать не только как корректирующий, но и как креативный инструмент обработки.

1 Устранение немузыкальных элементов

Как гул и мутность, мешающие частотам в нижнем низе прорваться через микс, шипящие и резкие звуки в районе 10 кГц отвлекают внимание от более важной высокочастотной информации в других точках частотного спектра. В зависимости от инструмента, различные немузыкальные звуки могут жить ниже 10 кГц.

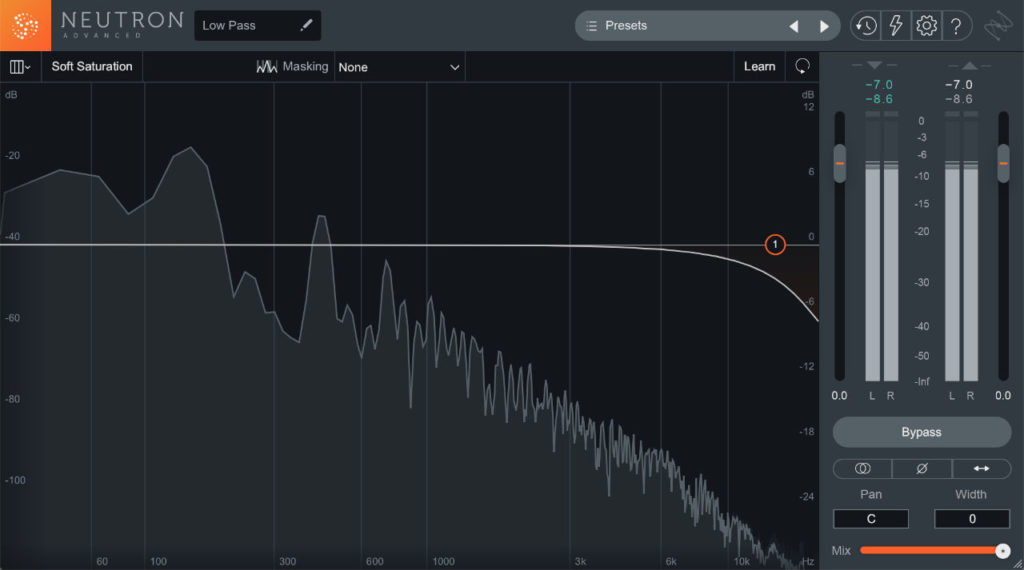
На скриншоте выше мы видим басовую линию с активированным эквалайзером Neutron. В этом конкретном случае интерес вызывает то, что происходит ниже 2 кГц. Обратите внимание на шумы, попавшие в сигнал во время записи — их наличие делает сигнал баса излишне активным в общем миксе. Когда мы повышаем громкость баса, существование таких помех становится критичным: шум усиливается вместе с сигналом и даже маскирует за собой другие инструменты.

Слушателю незачем слышать шум, ему не нужно знать, откуда он взялся и что вообще присутствует в сигнале. Задача звукорежиссера в том, чтобы скрыть подобный контент от ушей посторонних и переключить внимание людей на то, что реально важно — звук баса. Здесь-то и нужен Low-Pass фильтр: наведя точку обрезки на место, где шум исчезает, мы скроем его в миксе. Главное не отфильтровать лишнего, иначе сигнал баса исказится и потеряет в естественности.

При фильтрации всегда соблюдайте баланс. Фильтр должен отрезать лишнее, но не изменить сам сигнал.

2 Придание глубины

Глубина микса — важный фактор качественной записи. Благодаря ей мы можем почувствовать, что инструменты на переднем и заднем плане звуковой картины находятся на разном расстоянии. Обычно на переднем плане оставляют голос и вокал, ударные и гитары. На задний план отодвигают перкуссию, пэды и клавишные.

Мы привыкли, что в повседневной жизни объекты, находящиеся далеко от нас, звучат более тихо и менее ярко. Когда мы идём по улице, то двигатели и сигналы автомобилей звучат достаточно глухо. Несмотря на то, что в звуке двигателя преобладают низкие частоты, а в сигнале клаксона — высокие, когда мы находимся на некотором удалении от этих источников звука сигналы сливаются между собой в единую глухую картинку.

Этот принцип работает и при сведении музыки. Фильтруя верхний верх и снижая уровень инструментов, мы отодвигаем их на задний план микса.

Положение инструмента в миксе можно автоматизировать. Для этого достаточно активировать на дорожке Low-Pass фильтр и запрограммировать его так, чтобы в нужные моменты микса (например, в припеве) он отодвигал точку обрезки и выдвигал сигнал вперёд. Затем фильтр можно вернуть обратно, чтобы инструмент снова переехал на задний план. Благодаря автоматизации, о которой мы подробно рассказывали здесь, фильтр превращается из ограничивающего в креативный инструмент.

3 Устранение сталкивающихся частот у инструментов со схожим звучанием

Фильтрация полезна при создании пространства для разных сигналов. С помощью Low-Pass фильтра звукорежиссёр может выборочно удалить высокие частоты, чтобы дать больше свободы звучащим высоко инструментам.

Представим, что в вашем проекте присутствует множество слоев вокала и ярких синтезаторов. Из-за того, что вокал и синтезаторы живут в одних и тех же (или очень близких) частотных диапазонах, их звук становится зажатым — сигналам попросту тесно вместе. В попытках исправить эту ситуацию начинающие звукорежиссеры обычно усиливают верхний верх у вокала так, чтобы он выделился на фоне остальных сигналов. Ход логичный, но неправильный: проблема тесноты только усиливается, микс становится ярким до боли в ушах .

На деле же решение значительно проще: отфильтровать частоты в районе верхнего верха в тех сигналах, которым они не нужны. По итогам фильтрации мы получим вместо излишне накаченного энергией звука более аккуратный и отполированный саунд. Посмотрите на свои синтезаторы: если тело их звука присутствует только в среднем диапазоне, отсеките верх — так вы освободите место вокалу. Яркий звук снейра (с характерным хрустящим призвуком) также может мешать вокалу, поэтому лёгкое «помутнение» звука точно пойдет на пользу миксу.

Мы постоянно слышим советы усилить в миксе то или это. Но не менее важен другой совет: в первую очередь думайте не об усилении, а о том, что можно ослабить или вовсе убрать в миксе.

Выявить частотный дисбаланс помогает модуль Tonal Balance Control, входящий в iZotope Neutron и Ozone. Для пущей простоты сравните свой микс с референс-треком, чтобы понять, где наблюдается перекос по частотам в вашем треке. При сравнении синими областями модуль показывает расхождение вашего микса с референс-треком: синие области — количество частот в вашем миксе, белые линии — уровень частот в референс-треке.

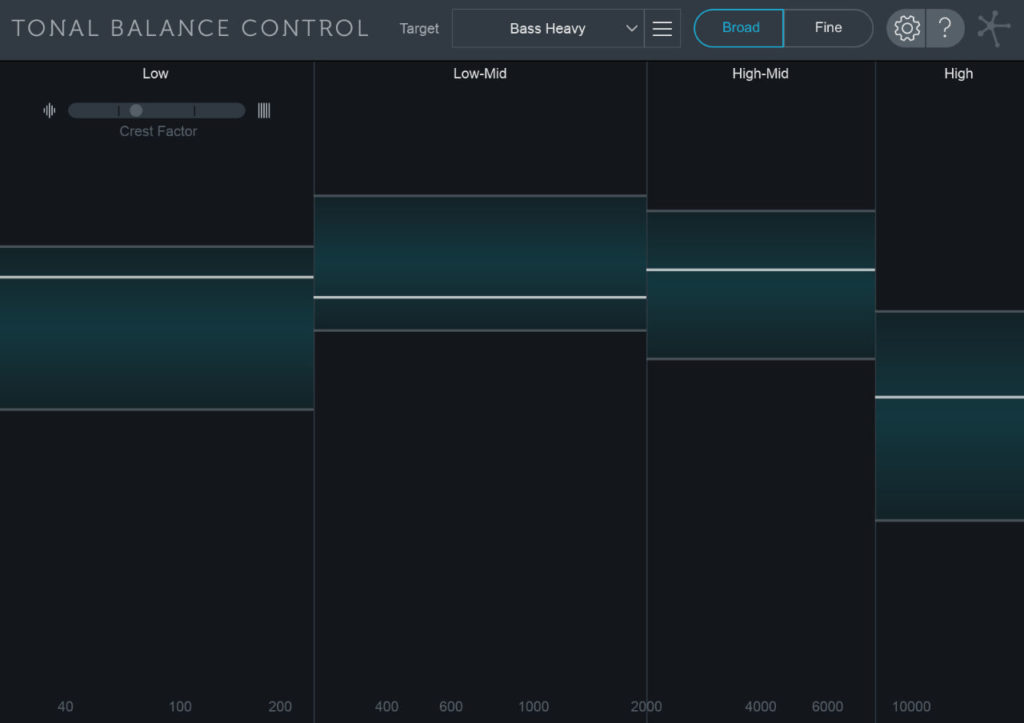
Если средние и высокие частоты выходят за верхнюю границу области, яркие элементы микса нужно откатить назад — отфильтровать сильнее. Если же эти частоты выходят за нижнюю границу или находятся около неё, то фильтрацию нужно ослабить — слишком активное ограничение не нужно.

4 Создание баланса между основным и бэк-вокалом

Чем больше вокальных дорожек в проекте, тем активнее частоты накладываются друг на друга и тем тяжелее что-либо разобрать в миксе. Пожалуй, самым мощным столкновением частот становится борьба добра со злом — основного и бэк-вокала.

Бэк-вокал всегда работает фоном и не должен конкурировать с основной вокальной партией за внимание слушателя. Чтобы освободить место основному вокалу, отфильтруйте Low-Pass фильтром бэк-вокал так, чтобы он стал похож на тень ведущего голоса. Скорее всего понадобится сделать ещё несколько подрезок в спектре, чтобы гармонично склеить две дорожки (это тема для отдельной статьи, которую мы обязательно напишем).

Если сбалансировать основной и бэк-вокал никак не получается, действуйте методом «от противного» — уменьшите количество вокальных дорожек в проекте. Слишком много однотипных треков с легкостью разрушает баланс микса, нарушает динамику и уменьшает доступный запас хедрума. Поэтому перед фильтрацией в первую очередь оцените, насколько вам нужно десять бэк-вокальных линий — правило «меньше — лучше» никто не отменял.

5 Выделение частот

Итак, мы знаем, что Low-Pass фильтр применяется для устранения частот. Тем не менее ему по силам не только устранять частоты, но и усиливать их в определённых границах. Благодаря этому можно аккуратно приручить инструменты в миксе, улучшив не только общую картину, но и подчеркнув интересные стороны их звучания.

Допустим, в сигнале присутствуют интересные верхние обертона, которые звучат слишком тихо. Поместив Low-Pass фильтр на дорожке и настроив точку обрезки на место, где обертона теряют энергию, мы можем без лишних проблем усилить их небольшим подъёмом. Активное задирание фильтра здесь не к чему: переусердствуете — середина станет звучать картонно, верх обязательно зашипит.

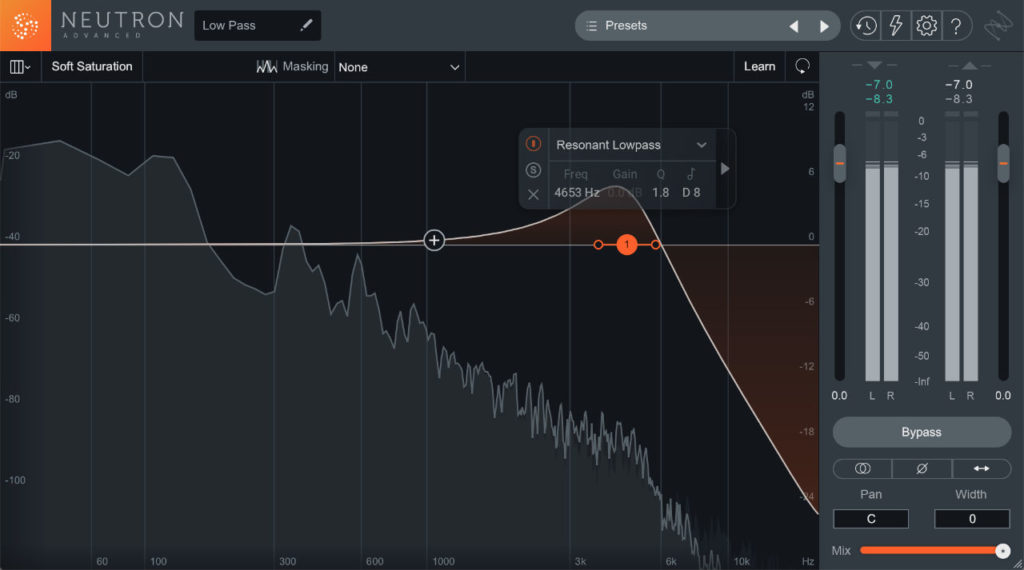
Чтобы избежать картонности и шипения, полагайтесь на буст широкой области частот вместо узкого точечного усиления. Широкий подъём усилит сигнал более естественно, а также минимизирует возможные искажения сигнала.

Тот же самый приём можно провести на другом конце спектра с помощью High-Pass фильтра. В этом случае речь идёт о подчеркивании гармоник и обертонов в низких частотах.

Пример программы для применения ФНЧ к сигналу переменного резистора

Напишем программу для Ардуино, которая будет считывать сигнал переменного резистора и накладывать на него ФНЧ с коэффициентом K = 0,1.

const byte potPin = A5; const float K = 0.1; float val = 0; void setup() < Serial.begin(9600); pinMode( potPin, INPUT ); >void loop()

Фильтрация сигнала акселерометра

Еще одним удачным примером использования ФНЧ может служить обработка сигнала акселерометра. Ниже представлены графики показаний акселерометра с применением фильтр и без, для разных K.

Источники шумов у акселерометра, отличаются от источников шума в цепи переменного резистора. Дело в том, что акселерометр регистрирует ускорение прибора, не различая, что явилось его причиной: сила гравитации или внешняя сила приложенная к датчику. Другими словами, если датчик находится в покое, то на него воздействует только сила гравитации, и мы легко узнаем углы наклона датчика относительно поверхности земли. Но если, например, датчик повернуть рукой вокруг одной оси, на него, кроме гравитации, подействует внешний момент силы, что приведет к ошибкам при расчете углов наклона. Другой источник шума — вибрация от двигателей, например, квадрокоптера.

Чтобы устранить эти шумы можно воспользоваться фильтром низких частот. Такая фильтрация значительно подавит вибрацию и прочие сильные скачки сигнала, вызванные кратковременным внешним воздействием на устройство.

Онлайн расчёт активных и пассивных фильтров

А не фильтрануть ли нам широким махом входной сигнал на предмет подавления помехи относительно единичного уровня на требуемой частоте, в заданное число раз отличающейся от границы полосы пропускания? А как насчёт расчёта активных полиномиальных фильтров второго порядка на звеньях Рауха, Сален-Ки и биквадратного звена? А кривую изменения реактивного сопротивления ёмкости в зависимости от частоты — не изобразить ли?
«Хватит умничать, пальцем покажи!», – предвижу я законное роптание посетителя, впавшего в соблазн от заголовка страницы. И действительно. Здесь нам не тут – базар надо фильтровать, а не безобразия нарушать!

Итак, приступим.
Для начала мы рассмотрим активные и пассивные ФНЧ, ФВЧ, ПФ без использования катушек индуктивности.

Определимся с терминологией:
– Фильтр нижних частот (ФНЧ) представляет собой устройство, которое пропускает сигналы низких частот и задерживает сигналы высоких частот.
– Фильтр верхних частот (ФВЧ) соответственно пропускает сигналы высоких частот и задерживает сигналы низких.
– Полосовой фильтр (ПФ) пропускает сигналы в некоторой полосе частот и подавляет сигналы и на низких частотах, и на высоких.
– Полоса пропускания определяется как диапазон частот, в котором АЧХ фильтра не выходит за пределы заданной неравномерности (обычно – 3дБ).
– Частотой среза фильтра называют частоту, ослабление сигнала на которой достигает -3дБ по логарифмической шкале, или 1/√2 ≈ 0.71 по линейной.
– Неравномерность АЧХ в полосе пропускания – размер флуктуации АЧХ от пика до пика в полосе пропускания.
– Крутизна частотной характеристики фильтра – скорость спада АЧХ в полосе подавления (дБ/октаву или дБ/декаду).

А начнём мы с простейших RC фильтров первого порядка. Слева фильтр нижних частот (ФНЧ), справа фильтр верхних частот (ФВЧ).

Рис.1 Схемы RC-фильтров первого порядка

Крутизна спада АЧХ таких фильтров в полосе подавления составляет 6 дБ/октаву.
Частота среза что ФВЧ, что ФНЧ рассчитывается по формуле: а и b — вещественные постоянные; m, n = 1,2,3…; n — определяет порядок фильтра.

Выше представленную формулу, для установившейся частот (р=jw) можно привести к следующему виду:

Отсюда фаз-частотная характеристика может быть представлена следующим образом:

$ф(w) = arctg(B(w) / A(w)$

Резонансная частота является частотой, на которой коэффициент передачи максимален для полосового фильтра или минимален для заграждающего фильтра. Добротность определяется отношением резонансной частоты к полосе пропускания.

Расчет активного фильтра нижних частот

Рассмотрим расчет параметров фильтра нижних частот на примере схемы, которая представлена ниже.

Рисунок 2. Схема. Автор24 — интернет-биржа студенческих работ

Коэффициент усиления напряжения рассчитывается по следующей формуле:

Усиление для фильтра нижних частот, представленного на рисунке выше, рассчитывается по следующей формуле:

Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ

где, Af — усиление в полосе пропускания (1 + R1 / R2); f — частота входного сигнала; fc — частота среза.

Коэффициент усиления будет изменяться в зависимости от частоты, которая подается на фильтр следующим образом:

1. Если f ∠ fc (очень низкие частоты), то Аv = Af
2. Если f = fc (частота равна частоте среза), то

Из данных выражений становится понятно, что у активного фильтра нижних частот коэффициент усиления находится в пределах от 0 Гц до частоты среза. А дальше, при повышении частоты, коэффициент усиления будет уменьшаться с постоянной скоростью.

Допустим, что нам необходимо рассчитать активный фильтр нижних частот, у которого коэффициент усиления равен 10, частота среза равняется 159 Гц, а входное сопротивление 10 кОм. Коэффициент усиления можно рассчитать по формуле:

Af = 1 + R1 / R2 = 10

Если предположить, что R1 = 1 кОм, то значение R2 будет равняться:

R2 = (10 — 1) • R1 = 9

Коэффициент усиления в децибелах рассчитывается следующим образом:

DB = 20 log Af = 20 log 10 = 20

Формула для расчета частоты среза выглядит следующим образом:

Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ

Зная, что fc = 159, а R = 10, можно вычислить емкость конденсатора:

C = 1 / (2п • fc • R) = 100