Обозначается напряженность магнитного поля буквой Н.
Если в катушку, по которой проходит ток I, внести сердечник из ферромагнитного материала (рис. 7.1г), то величина магнитной индукции В в каждой точке магнитного поля увеличивается, а напряженность Н в этих точках остается неизменной.
Разница между напряженностью Н и индукцией В в какой-либо точке магнитного поля (хотя обе величины характеризуют интенсивность магнитного поля) заключается в том, что напряженность в точке магнитного поля характеризует интенсивность поля в этой точке, созданного током без учета магнитной проницаемости среды, в которой создается поле, а индукция в этой точке характеризует интенсивность магнитного поля, созданного током и средой, которая намагничивается и изменяет его интенсивность; т. е. напряженность является расчетной величиной, не имеющей физического смысла, так как физически невозможно представить себе, что интенсивность поля не зависит от среды.
Таким образом, соотношение между В и H в какой-либо точке магнитного поля выглядит следующим образом:
т. к. μа характеризует способность среды намагничиваться. Следовательно, напряженность в этой точке
Из выражения (7.8) определяем единицу измерения напряженности в любой точке магнитного поля:
Напряженность — величина векторная, причем направление вектора напряженности в каждой точке совпадает с направлением магнитного поля в этой точке (касательная к магнитной линии в этой точке).
Если магнитное поле создано несколькими токами, то напряженность в каждой точке этого поля определяется геометрической суммой напряженностей, созданных каждым током в этой точке (рис. 7.5).
Очевидно, для каждой точки магнитного поля напряженность имеет определенную величину и направление.

6. Закон полного тока
Закон полного тока получен на основании многочисленных опытов. Этот закон устанавливает, что интеграл от напряженности магнитного поля по любому контуру (циркуляция вектора напряженности) равен алгебраической сумме тонов, сцепленных с этим контуром:
причем положительными следует считать те токи, направление которых соответствует обходу контура по направлению движения часовой стрелки (правило буравчика). В частности, для контура на рис. 7.6. по закону полного тока
Величина в (6.1) называется магнитодвижущей силой (сокращенно МДС).
Основной единицей измерения магнитодвижущей силы в системе СИ является ампер (А).
Магнитную цепь большинства электротехнических устройств можно представить состоящей из совокупности участков, в пределах каждого из которых можно считать магнитное поле однородным, т. е. с постоянной напряженностью, равной напряженности магнитного поля Hk, вдоль средней линии участка длиной lk. Для таких магнитных цепей можно заменить интегрирование в (6.1) суммированием.
ФИЗИКА. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ. ИС-19-3

Если при этом магнитное поле возбуждается катушкой с током I, у которой w витков, то для контура магнитной цепи, сцепленного с витками и состоящего из n участков, вместо (6.1) можно записать:
Таким образом, согласно закону полного тока МДС F равна сумме произведений напряженностей магнитного поля на длины соответствующих участков для контура магнитной цепи. Произведение часто называют магнитным напряжением участка магнитной цепи.
Характеристики магнитного поля
Напряженность магнитного поля (Н). Напряженность магнитного поля характеризует интенсивность поля в данной точке без учета среды, в которой создается магнитное поле, и является расчетной величиной. Кроме того, напряженность поля является векторной величиной. Вектор Н проводится по касательной к магнитным линиям (рис. 4.4).
Напряженность магнитного поля — это доля намагничивающей силы, приходящаяся на единицу длины магнитной линии. Напряжен

ность магнитного поля прямолинейного провода с током / в точке а на расстоянии R от его оси определяется по формуле

где / — длина магнитной линии с радиусом R.
Напряженность измеряется в амперах на метр:

Если напряженность во всех точках поля одинакова, то магнитное поле называется однородным.
Магнитное напряжение (UM). При расчете магнитных полей пользуются понятием магнитного напряжения. Для однородного магнитного поля магнитное напряжение Uu определяется по следующей формуле:

и измеряется в амперах:

Для неоднородного магнитного поля

Если магнитное напряжение UM вычисляется по замкнутому контуру, то его называют магнитодвижущей силой (МДС):

Магнитная индукция (В). Она характеризует интенсивность магнитного поля с учетом среды. Например, если внести внутрь катушки стальной сердечник, то интенсивность поля внутри катушки значительно возрастает за счет молекулярных круговых токов сердечника.
Магнитная индукция характеризует силовое воздействие магнитного поля на движущиеся электрические заряды (ток) и является силовой характеристикой магнитного поля аналогом напряженности электрического поля.
Магнитная индукция — это векторная величина. Вектор магнитной индукции проводится по касательной к магнитной линии в данной точке.
Магнитная индукция и напряженность магнитного поля связаны между собой соотношением

где )да — абсолютная магнитная проницаемость, характеризующая магнитные свойства среды, т.е. способность среды намагничиваться.
Абсолютная магнитная проницаемость вакуума ц0 называется магнитной постоянной:

Отношение абсолютной магнитной проницаемости к магнитной постоянной называется относительной магнитной проницаемостью, или просто магнитной проницаемостью р:

Например, магнитная проницаемость воздуха р = 1,000003.
Основной единицей измерения магнитной индукции является тесла (Тл):

Иногда используется более мелкая единица магнитной индукции гаусс (Гс):

Поток вектора магнитной индукции или магнитный поток (Ф). Произведение магнитной индукции однородного магнитного поля и такой плоской площадки S, во всех точках которой вектора индукции В одинаковы и перпендикулярны к ней, называется магнитным потоком:

Основной единицей измерения магнитного потока является вебер (Вб):

Иногда используют более мелкую единицу магнитного потока максвелл (Мкс):


Если вектор магнитной индукции не перпендикулярен площадке S (рис. 4.5), то определяют нормальную составляющую вектора Вп:

и тогда магнитный поток

В общем случае при определении магнитного потока через произвольную поверхность в неоднородном магнитном поле используют формулу

Магнитный поток как характеристика магнитного поля имеет в электротехнике большое значение при рассмотрении принципов работы электрических машин, трансформаторов и других электромагнитных устройств. Обмотки (катушки) этих устройств образуют w витков, каждый из которых пронизан (сцеплен) с магнитным потоком. Алгебраическая сумма этих магнитных потоков называется потоко- сцеплением ЧР:


Для катушек можно считать, что Ф, = Ф2 =. = Ф„„ тогда где Ф — магнитный поток, сцепленный с одним из витков.
Контрольные вопросы и задания
- 1. Перечислите характеристики магнитного поля.
- 2. Что характеризует напряженность магнитного поля?
- 3. Напишите формулу напряженности магнитного поля и укажите единицу ее измерения.
- 4. Напишите формулу магнитного напряжения для однородного магнитного поля и укажите единицу его измерения.
- 5. Как называется магнитное напряжение UM, если оно вычисляется по замкнутому контуру?
- 6. Объясните разницу между напряженностью Н и индукцией В магнитного поля.
- 7. Какая из характеристик является силовой характеристикой магнитного поля?
- 8. Напишите формулу магнитной индукции и укажите единицу ее измерения.
- 9. Напишите формулу связи между величинами ца, ц0 и Ц.
- 10. Что называют магнитным потоком?
- 11. Напишите формулу магнитного потока для однородного магнитного поля и укажите единицу его измерения.
- 12. Что называют потокосцеплением?
Напряжённость магнитного поля

Напряжённость магни́тного по́ля, векторная физическая величина, определяемая равенством H = B μ 0 − M , boldsymbol = frac ><mu_0>-boldsymbol, H = μ 0 B − M , где B boldsymbol B – магнитная индукция , μ 0 – μ_0 – μ 0 – магнитная постоянная , M boldsymbol M – намагниченность среды. В случае вакуума M = 0 boldsymbol=0 M = 0 и B = μ 0 H , boldsymbol=μ_0boldsymbol, B = μ 0 H , т. е. векторы B boldsymbol B и M boldsymbol M отличаются друг от друга постоянным множителем. Напряжённость магнитного поля входит в одно из уравнений Максвелла : rot H = j + j см , text:boldsymbol=boldsymbol+boldsymbol>, rot H = j + j см , где j boldsymbol j – плотность тока проводимости , обусловленного перемещением электрических зарядов ; j см = ∂ D / ∂ t boldsymbol>= partial boldsymbol/ partial t j см = ∂ D / ∂ t – плотность тока смещения ; D boldsymbol D – вектор электрической индукции . Намагниченность среды M boldsymbol M связана с токами намагничивания – усреднёнными по физически малому объёму молекулярными токами (токами, связанными с движением электронов в молекулах вещества): rot M = j м , text:boldsymbol=boldsymbol, rot M = j м , где j м – boldsymbol – j м – плотность тока намагничивания. Напряжённость магнитного поля является удобной вспомогательной величиной, введение которой упрощает расчёт магнитного поля в веществе, т. к. в уравнение Максвелла для rot H text:boldsymbol rot H не входит плотность тока намагничивания j м , boldsymbol, j м , Для высокочастотных переменных электромагнитных полей разделение плотности тока намагничивания j м boldsymbol j м и плотности тока смещения j см boldsymbol> j см неоднозначно, поэтому и определение напряжённости магнитного поля в этом случае условно.
Исторически в качестве основного вектора для описания магнитного поля был выбран вектор H boldsymbol H , с чем и связано его название. Однако впоследствии оказалось, что основным вектором следует считать вектор магнитной индукции B boldsymbol B , который определяет силовое воздействие магнитного поля на движущийся электрический заряд (см. статью Сила Лоренца ). Для изотропных неферромагнитных сред в случае слабых магнитных полей напряжённость магнитного поля H boldsymbol H и намагниченность M boldsymbol M связаны соотношением M = χ H , boldsymbol=χboldsymbol, M = χ H , где χ – χ – χ – магнитная восприимчивость среды. При этом B = μ μ 0 H , boldsymbol=μμ_0boldsymbol, B = μ μ 0 H , где μ = 1 + χ – μ=1+χ – μ = 1 + χ – магнитная проницаемость среды. Для ферромагнетиков χ χ χ и μ μ μ зависят от напряжённости магнитного поля.
Опубликовано 21 ноября 2023 г. в 10:46 (GMT+3). Последнее обновление 21 ноября 2023 г. в 10:46 (GMT+3). Связаться с редакцией
Информация

Области знаний: Магнитное поле
Закон Био-Савара-Лапласа
Это важнейший в электромагнетизме закон. Он определяет вектор напряженности $d bar$ в произвольной точке магнитного поля, которое создает в вакууме элементарный проводник длинны dl с постоянным током I:
где $d bar$ – вектор элемента проводника, который по модулю равен длине проводника, направление совпадает с направлением тока; $bar$ – радиус–вектор, который проводят от рассматриваемого элементарного проводника к точке рассмотрения поля; $r=|bar|$ .
Вектор $d bar$ – перпендикулярен плоскости, в которой находятся векторы $d bar$ и $bar$, и направлен так, что из его конца вращение вектора $d bar$ по кратчайшему пути до совмещения с вектором $bar$ происходило по часовой стрелке. Для нахождения направления вектора $d bar$ можно использовать правило буравчика (Буравчик (винт) вращаем так, чтобы его поступательное движение совпадало с направлением тока, тогда направление, по которому вращается ручка винта, совпадает с направлением вектора напряженности поля, которое создает рассматриваемый ток).
Закон Био-Савара-Лапласа дает возможность вычислять величину полной напряженности магнитного поля, которое создает ток, текущий по проводнику любой формы.
Для нахождения полной напряженности магнитного поля, которое создает в исследуемой точке ток I, который течет по проводнику l, следует векторно суммировать все элементарные напряженности $d bar$, порождаемые элементами проводника и найденные по формуле (4).
Единицы измерения
Основной единицей измерения момента силы в системе СИ является: [H]=А/м
Задание. Чему равна напряженность (H) в центре кругового витка (R — радиус витка) с током I.
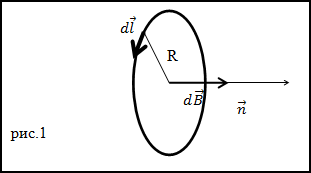
Решение. Каждый элементарный ток витка магнитное поле в центре окружности, напряженность которого направлена по положительной нормали к плоскости контура витка (рис.1). Поэтому, если элементарную напряженность поля найти по закону Био-Савара – Лапласа, то векторное сложение элементарных полей можно будет заменить на алгебраическое.
В соответствии с законом Био-Савара – Лапласа dH равно:
Применяя выражение (1.1) к нашему случаю, получим:
Возьмем интеграл по контуру, получим:
Ответ. $H=frac$

проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Задание. Какова напряженность магнитного поля, которую создает электрон, движущийся прямолинейно и равномерно со скоростью v? Если точка, в которой исследуется поле, находится на расстоянии r от электрона на перпендикуляре к вектору скорости, если перпендикуляр провести через мгновенное положение частицы.
Решение. Сделаем рисунок.
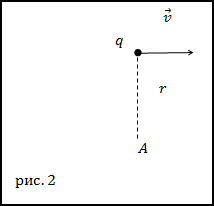
Напряженность магнитного поля будем искать, применяя закон Био – Савара – Лапласа:
Если все заряды одинаковы (q), то плотность тока равна:
заряд отрицательный, следовательно, направления векторов $bar$ и $bar$ противоположны. n – концентрация зарядов. Подставим формулу (2.3) в (2.2), результат в (2.1) получаем:
где dN=Sdln — количество заряженных частиц в отрезке dl. В таком случае, напряженность поля, которое создает один заряд:
По условию задачи $bar perp bar$ , значит модуль напряжённости магнитного поля в точке А (рис.2) будет равен:
Напряженность магнитного поля в центре витка с током
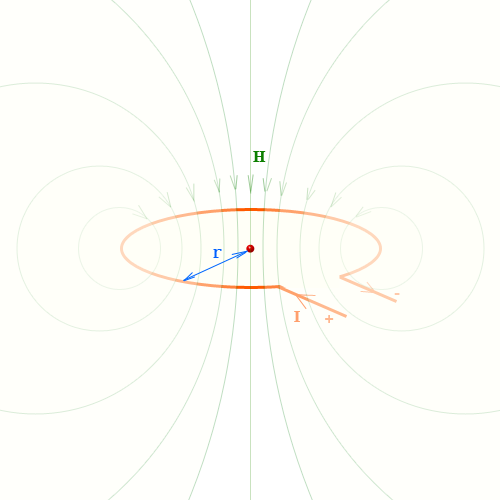
Напряженность магнитного поля в центре витка с током
| напряженность магнитного поля в центре витка с током, | Ампер/метр |
| сила тока в витке, | Ампер |
| радиус витка, | метр |
то напряженность магнитного поля определяется формулой
Напряженность магнитного поля
Напряженность магнитного поля необходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах. Напряженность магнитного поля характеризует магнитное поле в вакууме.
Напряженность магнитного поля [ H ] – это отношение магнитной индукции к магнитной проницаемости среды
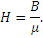
Напряженность магнитного поля – величина векторная. За единицу измерения напряженности магнитного поля в Международной системе единиц принят ампер на метр.
Напряженность магнитного поля (формула) векторная физическая величина, равная:
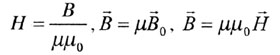
Напряженность магнитного поля в СИ — ампер на метр (А/м).
Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поля в данной точке, то можно определить индукцию поля в этой точке.
Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии.
Обобщая экспериментальные данные французских физиков Био и Савара, Лаплас (французский математик) предложил формулу, по которой можно вычислять напряженность поля, создаваемого элементом тока в точке, расположенной от этого элемента на расстоянии r.
Измерение напряженности магнитного поля
Для практических измерений H в лаборатории или полевых условиях используются специальные приборы — магнитометры. Различают магнитометры скалярные (измеряющие модуль H) и векторные (дающие полную информацию о направлении и величине).
Существуют индукционные, феррозондовые, квантовые, СКВИД и другие типы магнитометров. Их чувствительность может достигать 10-15 Тл, что позволяет регистрировать даже очень слабые магнитные поля.
Перспективы использования напряженности магнитного поля
Управление напряженностью H открывает большие возможности для развития новых технологий. Например, в медицине при лечении рака или других заболеваний.
Также идут работы по созданию магнитных движителей для транспорта, где используются сильные неоднородные поля. В будущем появятся и другие интересные применения H.




