Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной .
Механические волны бывают разных видов. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной . Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне.
Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной . Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн.
Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.
Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.
Распространение поперечного волнового импульса по натянутому резиновому жгуту
Распространение продольного волнового импульса по упругому стержню
Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами . В реальных средах эти свойства распределены по всему объему. Так, например, любой малый элемент твердого тела обладает массой и упругостью. В простейшей одномерной модели твердое тело можно представить как совокупность шариков и пружинок (рис. 2.6.3).
Простейшая одномерная модель твердого тела
В этой модели инертные и упругие свойства разделены. Шарики обладают массой , а пружинки – жесткостью . С помощью такой простой модели можно описать распространение продольных и поперечных волн в твердом теле. В продольных волнах шарики испытывают смещения вдоль цепочки, а пружинки растягиваются или сжимаются. Такая деформация называется деформацией растяжения или сжатия (см. §1.12). В жидкостях или газах деформация такого рода сопровождается уплотнением или разрежением .
Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
Если в одномерной модели твердого тела один или несколько шариков сместить в направлении, перпендикулярном цепочке, то возникнет деформация сдвига . Деформированные при таком смещении пружины будут стремиться возвратить смещенные частицы в положение равновесия. При этом на ближайшие несмещенные частицы будут действовать упругие силы, стремящиеся отклонить их от положения равновесия. В результате вдоль цепочки побежит поперечная волна.
Волны. Основные понятия. Решение задач.Задача 1
В жидкостях и газах упругая деформация сдвига не возникает. Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появится. Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. То же относится к газообразной среде. Следовательно, поперечные волны не могут существовать в жидкой или газообразной средах .
Значительный интерес для практики представляют простые гармонические или синусоидальные волны . Они характеризуются амплитудой колебания частиц, частотой и длиной волны . Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью .
Смещение частиц среды из положения равновесия в синусоидальной волне зависит от координаты на оси , вдоль которой распространяется волна, и от времени по закону:
где – так называемое волновое число , – круговая частота.
На рис. 2.6.4 изображены «моментальные фотографии» поперечной волны в два момента времени: и . За время волна переместилась вдоль оси на расстояние . Такие волны принято называть бегущими (в отличие от стоячих волн, см. далее).
«Моментальные фотографии» бегущей синусоидальной волны в момент времени и
Длиной волны называют расстояние между двумя соседними точками на оси , колеблющимися в одинаковых фазах. Расстояние, равное длине волны , волна пробегает за период , следовательно, , где – скорость распространения волны.
Для любой выбранной точки на графике волнового процесса (например, для точки на рис. 2.6.4) с течением времени изменяется координата этой точки, а значение выражения не изменяется. Через промежуток времени точка переместится по оси на некоторое расстояние . Следовательно:
Таким образом, бегущая синусоидальная волна обладает двойной периодичностью – во времени и пространстве. Временной период равен периоду колебаний частиц среды, пространственный период равен длине волны . Волновое число является пространственным аналогом круговой частоты
Обратим внимание на то, что уравнение
описывает синусоидальную волну, распространяющуюся в направлении, противоположном направлению оси , со скоростью
В бегущей синусоидальной волне каждая частица среды совершает гармонические колебания с некоторой частотой . Поэтому, как и в случае простого колебательного процесса, средняя потенциальная энергия, запасенная в некотором объеме среды, равна средней кинетической энергии в том же объеме и пропорциональна квадрату амплитуды колебаний.
Отсюда следует, что при распространении бегущей волны возникает поток энергии, пропорциональный скорости волны и квадрату ее амплитуды.
Бегущие волны распространяются в средах с определенными скоростями, зависящими от типа волны, а также от инертных и упругих свойств среды.
Скорость поперечных волн в натянутой струне или резиновом жгуте зависит от погонной массы (т. е. массы единицы длины) и силы натяжения :
Скорость распространения продольных волн в безграничной среде определяется плотностью среды (т. е. массой единицы объема) и модулем всестороннего сжатия , который равен коэффициенту пропорциональности между изменением давления и относительным изменением объема , взятому с обратным знаком:
Выражение для скорости распространения продольных волн в безграничных средах имеет вид
Например, при температуре скорость распространения продольных волн в воде , в различных сортах стали .
При распространении продольных волн в упругих стержнях в формулу для скорости волн вместо модуля всестороннего сжатия входит модуль Юнга (см. §1.12):
Для стали отличие от невелико, для других материалов оно может составлять и даже больше.
Модель. Продольные и поперечные волны
Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения ( суперпозиции ) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.
Если волны, бегущие по струне во встречных направлениях, имеют синусоидальную форму, то при определенных условиях они могут образовать стоячую волну .
Пусть струна длины закреплена так, что один из ее концов находится в точке , а другой – в точке (рис. 2.6.5). В струне создано натяжение .
Образование стоячей волны в струне, закрепленной на обоих концах
По струне одновременно распространяются в противоположных направлениях две волны одной и той же частоты:
- – волна, бегущая справа налево;
- – волна, бегущая слева направо.
В точке (один из закрепленных концов струны) падающая волна в результате отражения порождает волну . При отражении от неподвижно закрепленного конца отраженная волна оказывается в противофазе с падающей. Согласно принципу суперпозиции , который является экспериментальным фактом, колебания, вызванные встречными волнами в каждой точке струны, складываются. Таким образом, результирующее колебание в каждой точке равно сумме колебаний, вызванных волнами 1 и 2 в отдельности. Следовательно,
Это и есть стоячая волна . В стоячей волне существуют неподвижные точки, которые называются узлами . Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями .
Оба неподвижных конца струны должны быть узлами. Приведенная выше формула удовлетворяет этому условию на левом конце (). Для выполнения этого условия и на правом конце (), необходимо чтобы , где – любое целое число. Это означает, что стоячая волна в струне возникает не всегда, а только в том случае, если длина струны равняется целому числу длин полуволн:
Набору значений длин волн соответствует набор возможных частот :
где – скорость распространения поперечных волн по струне. Каждая из частот и связанный с ней тип колебания струны называется нормальной модой . Наименьшая частота называется основной частотой , все остальные () называются гармониками . На рис. 2.6.5 изображена нормальная мода для .
В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не транспортируется в другие части струны. В каждом таком отрезке происходит периодическое (дважды за период ) превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Но в отличие от груза на пружине или маятника, у которых имеется единственная собственная частота струна обладает бесконечным числом собственных (резонансных) частот . На рис. 2.6.6 изображены несколько типов стоячих волн в струне, закрепленной на обоих концах.
Первые пять нормальных мод колебаний струны, закрепленной на обоих концах
В соответствии с принципом суперпозиции стоячие волны различных типов (т. е. с разными значениями ) могут одновременно присутствовать в колебаниях струны.
Скорость и длина волны
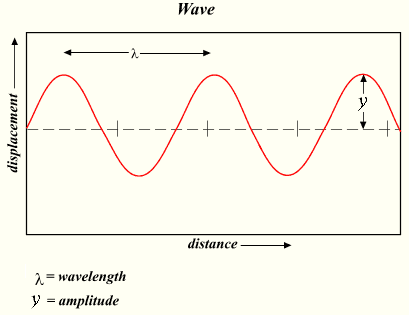
Если бросить камень в воду, то в месте его падения частицы воды начинают колебаться, двигаясь вверх и вниз. Соседние частицы, связанные с ними силами сцепления, также приходят в колебание. Однако для передачи колебания соседним частицам требуется некоторое время. То есть, чем дальше отстоят частицы от места, где начались колебания, тем позже эти частицы будут вовлечены в колебательное движение. Таким образом, от места падения камня волна бежит во все стороны с определенной скоростью, которая называется скоростью распространения волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. Если считать скорость волны постоянной, то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
Так как период колебаний в волне обратно пропорционален частоте,
то можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:
Калькулятор ниже позволяет по двум известным параметрам формулы посчитать неизвестный.
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Связь со скоростью
Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).
Формула скорости
𝑣 = S/t
Переходя к волнам, можно провести следующие аналогии:
- путь — длина волны
- время — период
А для скорости даже аналогия не нужна — скорость и в Африке скорость.
Формула скорости волны
𝑣 = λ/T
λ — длина волны [м]
Задачка
Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
Решение:
Возьмем формулу скорости:

Резонанс
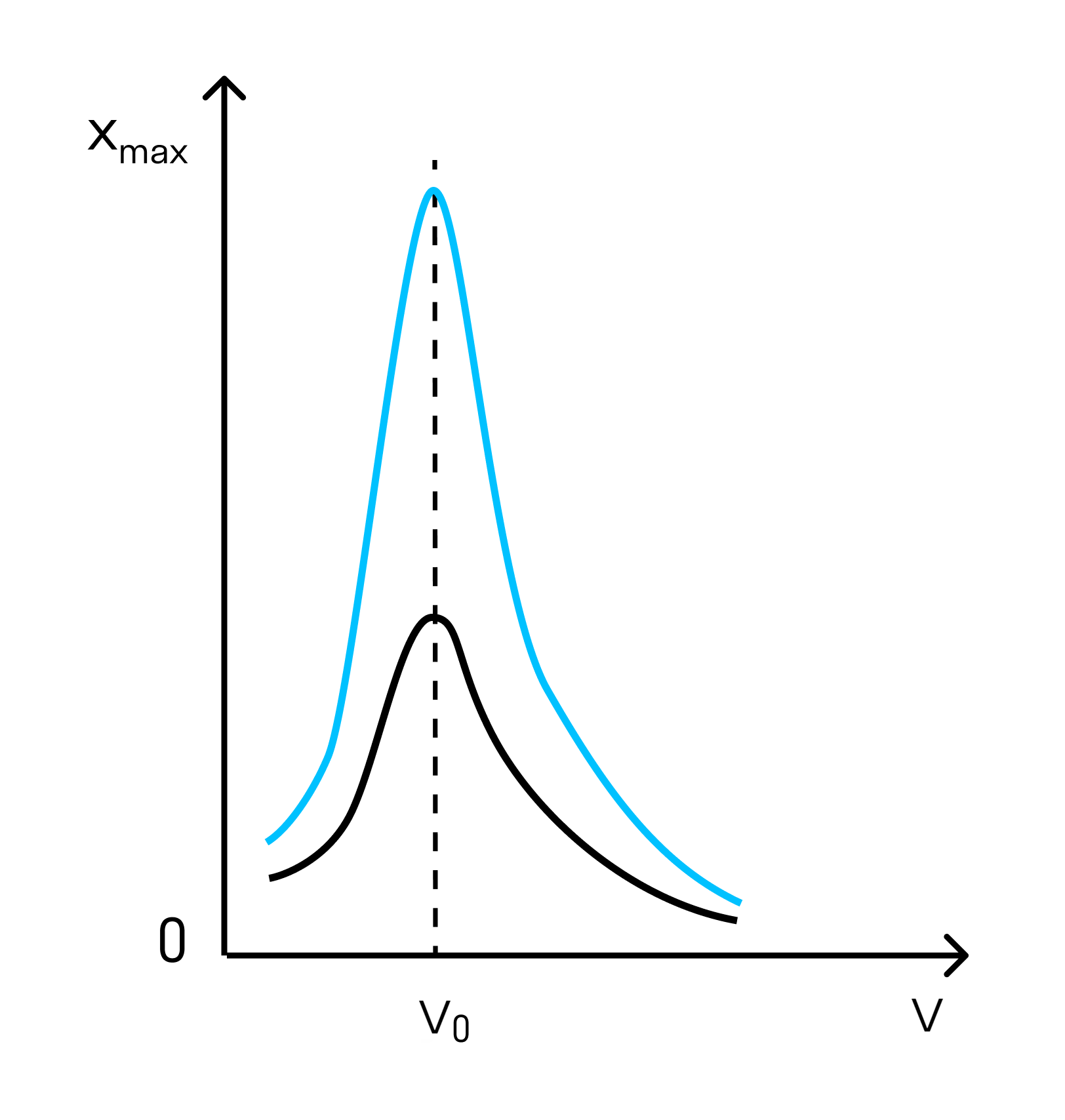
Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.
На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.
Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.
Формула частоты
ν = N/t
N — количество колебаний [—]
В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст
Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.
В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.
Скорость и длина волны
Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Помимо скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.

Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
где
v — скорость волны; T — период колебаний в волне; λ (греческая буква «ламбда») — длина волны.
Выбрав направление распространения волны за направление оси x и обозначив через y координату колеблющихся в волне частиц, можно построить график волны. График синусоидальной волны (при фиксированном времени t) изображен на рисунке 45. Расстояние между соседними гребнями (или впадинами) на этом графике совпадает с длиной волны λ.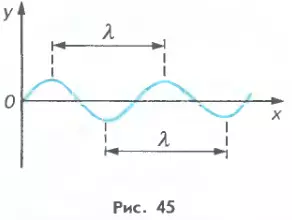
Формула (22.1) выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте, т. е. T = 1/ν, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой: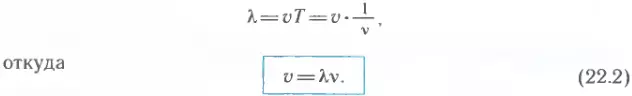
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
1. Что понимают под скоростью волны? 2. Что такое длина волны? 3. Как длина волны связана со скоростью и периодом колебаний в волне? 4. Как длина волны связана со скоростью и частотой колебаний в волне? 5. Какие из следующих характеристик волны изменяются при переходе волны из одной среды в другую: а) частота; б) период; в) скорость; г) длина волны?
Экспериментальное задание. Налейте воду в ванну и посредством ритмичных касаний воды пальцем (или линейкой) создайте на ее поверхности волны. Используя разную частоту колебаний (например, касаясь воды один и два раза в секунду), обратите внимание на расстояние между соседними гребнями волн. При какой частоте колебаний длина волны больше?
Длина волны через период
Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной .
Механические волны бывают разных видов. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной . Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне.
Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной . Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн.
Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.
Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.
Распространение поперечного волнового импульса по натянутому резиновому жгуту
Распространение продольного волнового импульса по упругому стержню
Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами . В реальных средах эти свойства распределены по всему объему. Так, например, любой малый элемент твердого тела обладает массой и упругостью. В простейшей одномерной модели твердое тело можно представить как совокупность шариков и пружинок (рис. 2.6.3).
Простейшая одномерная модель твердого тела
В этой модели инертные и упругие свойства разделены. Шарики обладают массой , а пружинки – жесткостью . С помощью такой простой модели можно описать распространение продольных и поперечных волн в твердом теле. В продольных волнах шарики испытывают смещения вдоль цепочки, а пружинки растягиваются или сжимаются. Такая деформация называется деформацией растяжения или сжатия (см. §1.12). В жидкостях или газах деформация такого рода сопровождается уплотнением или разрежением .
Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
Если в одномерной модели твердого тела один или несколько шариков сместить в направлении, перпендикулярном цепочке, то возникнет деформация сдвига . Деформированные при таком смещении пружины будут стремиться возвратить смещенные частицы в положение равновесия. При этом на ближайшие несмещенные частицы будут действовать упругие силы, стремящиеся отклонить их от положения равновесия. В результате вдоль цепочки побежит поперечная волна.
В жидкостях и газах упругая деформация сдвига не возникает. Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появится. Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. То же относится к газообразной среде. Следовательно, поперечные волны не могут существовать в жидкой или газообразной средах .
Значительный интерес для практики представляют простые гармонические или синусоидальные волны . Они характеризуются амплитудой колебания частиц, частотой и длиной волны . Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью .
Смещение частиц среды из положения равновесия в синусоидальной волне зависит от координаты на оси , вдоль которой распространяется волна, и от времени по закону:
где – так называемое волновое число , – круговая частота.
На рис. 2.6.4 изображены «моментальные фотографии» поперечной волны в два момента времени: и . За время волна переместилась вдоль оси на расстояние . Такие волны принято называть бегущими (в отличие от стоячих волн, см. далее).
«Моментальные фотографии» бегущей синусоидальной волны в момент времени и
Длиной волны называют расстояние между двумя соседними точками на оси , колеблющимися в одинаковых фазах. Расстояние, равное длине волны , волна пробегает за период , следовательно, , где – скорость распространения волны.
Для любой выбранной точки на графике волнового процесса (например, для точки на рис. 2.6.4) с течением времени изменяется координата этой точки, а значение выражения не изменяется. Через промежуток времени точка переместится по оси на некоторое расстояние . Следовательно:
Таким образом, бегущая синусоидальная волна обладает двойной периодичностью – во времени и пространстве. Временной период равен периоду колебаний частиц среды, пространственный период равен длине волны . Волновое число является пространственным аналогом круговой частоты
Обратим внимание на то, что уравнение
описывает синусоидальную волну, распространяющуюся в направлении, противоположном направлению оси , со скоростью
В бегущей синусоидальной волне каждая частица среды совершает гармонические колебания с некоторой частотой . Поэтому, как и в случае простого колебательного процесса, средняя потенциальная энергия, запасенная в некотором объеме среды, равна средней кинетической энергии в том же объеме и пропорциональна квадрату амплитуды колебаний.
Отсюда следует, что при распространении бегущей волны возникает поток энергии, пропорциональный скорости волны и квадрату ее амплитуды.
Бегущие волны распространяются в средах с определенными скоростями, зависящими от типа волны, а также от инертных и упругих свойств среды.
Скорость поперечных волн в натянутой струне или резиновом жгуте зависит от погонной массы (т. е. массы единицы длины) и силы натяжения :
Скорость распространения продольных волн в безграничной среде определяется плотностью среды (т. е. массой единицы объема) и модулем всестороннего сжатия , который равен коэффициенту пропорциональности между изменением давления и относительным изменением объема , взятому с обратным знаком:
Выражение для скорости распространения продольных волн в безграничных средах имеет вид
Например, при температуре скорость распространения продольных волн в воде , в различных сортах стали .
При распространении продольных волн в упругих стержнях в формулу для скорости волн вместо модуля всестороннего сжатия входит модуль Юнга (см. §1.12):
Для стали отличие от невелико, для других материалов оно может составлять и даже больше.
Модель. Продольные и поперечные волны
Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения ( суперпозиции ) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.
Если волны, бегущие по струне во встречных направлениях, имеют синусоидальную форму, то при определенных условиях они могут образовать стоячую волну .
Пусть струна длины закреплена так, что один из ее концов находится в точке , а другой – в точке (рис. 2.6.5). В струне создано натяжение .
Образование стоячей волны в струне, закрепленной на обоих концах
По струне одновременно распространяются в противоположных направлениях две волны одной и той же частоты:
- – волна, бегущая справа налево;
- – волна, бегущая слева направо.
В точке (один из закрепленных концов струны) падающая волна в результате отражения порождает волну . При отражении от неподвижно закрепленного конца отраженная волна оказывается в противофазе с падающей. Согласно принципу суперпозиции , который является экспериментальным фактом, колебания, вызванные встречными волнами в каждой точке струны, складываются. Таким образом, результирующее колебание в каждой точке равно сумме колебаний, вызванных волнами 1 и 2 в отдельности. Следовательно,
Это и есть стоячая волна . В стоячей волне существуют неподвижные точки, которые называются узлами . Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями .
Оба неподвижных конца струны должны быть узлами. Приведенная выше формула удовлетворяет этому условию на левом конце (). Для выполнения этого условия и на правом конце (), необходимо чтобы , где – любое целое число. Это означает, что стоячая волна в струне возникает не всегда, а только в том случае, если длина струны равняется целому числу длин полуволн:
Набору значений длин волн соответствует набор возможных частот :
где – скорость распространения поперечных волн по струне. Каждая из частот и связанный с ней тип колебания струны называется нормальной модой . Наименьшая частота называется основной частотой , все остальные () называются гармониками . На рис. 2.6.5 изображена нормальная мода для .
В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не транспортируется в другие части струны. В каждом таком отрезке происходит периодическое (дважды за период ) превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Но в отличие от груза на пружине или маятника, у которых имеется единственная собственная частота струна обладает бесконечным числом собственных (резонансных) частот . На рис. 2.6.6 изображены несколько типов стоячих волн в струне, закрепленной на обоих концах.
Первые пять нормальных мод колебаний струны, закрепленной на обоих концах
В соответствии с принципом суперпозиции стоячие волны различных типов (т. е. с разными значениями ) могут одновременно присутствовать в колебаниях струны.
Длина волны через период
«Физика — 11 класс»
За один период волна распространяется на расстояние λ.

λ = vT
Длина волны — это расстояние, на которое распространяется волна за время, равное одному периоду колебаний.
Так как период Т и частота v связаны соотношением

При распространении волны:
1. Каждая частица шнура совершает периодические колебания во времени.
В случае гармонических колебаний (по закону синуса или косинуса) частота и амплитуда колебаний частиц одинаковы во всех точках шнура.
Эти колебания различаются только фазами.
2. В каждый момент времени форма волны повторяется через отрезки длиной λ.

Спустя промежуток времени Δt волна будет иметь вид, изображенный на том же рисунке второй линией.
Для продольной волны также справедлива формула, связывающая скорость распространения волны, длину волны и частоту колебаний.
Все волны распространяются с конечной скоростью. Длина волны зависит от скорости ее распространения и частоты колебаний.
Уравнение гармонической бегущей волны
Вывод уравнения волны, позволяющего определить смещение каждой точки среды в любой момент времени при распространении гармонической волны (на примере поперечной волны, бегущей по длинному тонкому резиновому шнуру).
Ось ОХ направлена вдоль шнура.
Начало отсчета — левый конец шнура.
Смещение колеблющейся точки шнура от положения равновесия — s.
Для описания волнового процесса нужно знать смещение каждой точки шнура в любой момент времени:
s = s (х, t).
Конец шнура (точка с координатой х = 0) совершает гармонические колебания с циклической частотой ω.
Колебания этой точки будут происходят по закону:
s = sm sinc ωt
Если начальную фазу колебаний считать равной нулю.
sm — амплитуда колебаний.

Колебания распространяются вдоль оси ОХ со скоростью υ и в произвольную точку с координатой х придут спустя время

Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ.

Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой sm, но с другой фазой:

Это и есть уравнение гармонической бегущей волны, распространяющейся в положительном направлении оси ОХ.
Используя уравнение можно определить смещение различных точек шнура в любой момент времени.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Следующая страница «Распространение волн в упругих средах»
Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»
Механические волны. Физика, учебник для 11 класса — Класс!ная физика




