Переменный ток, как и постоянный, оказывает тепловое, механическое, магнитное и химическое действие. В формулы расчета теплового, механического, магнитного, и химического действия переменного тока. Действующим значением переменного тока называется постоянный ток, который за время одного периода оказывает такое тепловое (механическое и др.) действие, как и данный переменный ток. Действующее значение для данного переменного тока есть величина постоянная и
равная амплитудному значению, деленному на , т.е.
Для доказательства этого рассмотрим тепловое действие тока.
Тепловое действие постоянного тока определяется по закону Джоуля – Ленца:
где Т – время, равное одному периоду.
Такое же количество теплоты в данном проводнике за это время выделится при переменном токе
i = I m sinωt . Тогда формула (3.2) для переменного тока примет вид:
где I – действующее значение переменного тока.
Из формулы (3.3) можно записать:
где Р – средняя мощность переменного тока за период. Мгновенная мощность синусоидального тока равна:
Как видно из формулы (3.5), мгновенная мощность переменного тока выражается двумя слагаемыми. Первое слагаемое является величиной постоянной и от времени не зависит, а второе – изменяется по синусоидальному закону и в сумме за период равно нулю.
Следовательно, средняя мощность переменного тока может быть выражена формулой:
Из равенства (3.4) и (3.6) можно записать:
Все определения и соотношения действующего значения переменного тока справедливы и для переменного напряжения и ЭДС.
Амперметры и вольтметры при изменении переменного тока и напряжения чаще всего показывают их действующие значения, так как принцип работы их основан на механическом или тепловом действии тока.
Определим амплитудное значение напряжения в сети, если при сопротивлении цепи 40 Ом амперметр показывает ток 5,5 А.
Из закона Ома напряжение равно U = IR. Подставим вместо I и R их значения, получим действующее значение напряжения U=5,5·40 = 220 B, а так как то U m =1,41·220 = 310,2 B.
В электротехнике при расчете выпрямителей и электрических машин приходится иметь дело со средними значениями переменного тока. Для переменного тока, изменяющегося по синусоидальному закону, среднее значение тока за период будет равно нулю. Поэтому среднее значение синусоидального закона тока (ЭДС, напряжения) определяется за половину периода. Средним значением силы переменного тока (ЭДС, напряжения) называется среднее значение из всех мгновенных значений силы тока (ЭДС, напряжения) за положительный полупериод. Для синусоидального тока
Аналогично определяются средние значения синусоидальных переменных ЭДС и напряжений.
Ток, ЭДС и напряжение, меняющиеся по синусоидальному закону, можно представить как проекцию радиус-вектора, вращающегося против часовой стрелки с постоянной угловой скоростью ω и равного по модулю амплитудному значению этих величин (рис.3.2, a).
лекция 407 действующее значение напряжения


![]()
![]()
![]()


Проекция радиус-вектора на ось y запишется в таком виде:
U y = U m sinωt (3.9)
Если изменение проекции радиус-вектора напряжения со временем развернуть на плоскости, то получим синусоиду (рис. 3.2, б ).
В случае, когда в начальный момент радиус-вектор не лежит на оси x, а смещен на угол ψ по ходу его вращения, то его проекция на ось y запишется так:
U y = U m sin(ωt+ψ) (3.10)
Когда же в начальный момент времени радиус-вектор повернут относительно оси x на угол ψ против направления вращения радиус-вектора, то проекция его на ось y выразится:
U y = U m sin(ωt+ψ) (3.10)
Из геометрии известно, что алгебраическая сумма проекций двух векторов равна проекции вектора, представляющего сумму данных векторов. Следовательно, сложение одноименных синусоидальных электрических величин (проекций векторов) можно осуществить сложением векторов, представляющих амплитудные значения этих электрических величин. При этом наглядно представляется не только сумма или разность векторов, но и сдвиг фаз между электрическими величинами.
Совокупность векторов, изображающих действующее или амплитудные значения синусоидальных электрических величин, представляет собой векторную диаграмму.
При построении векторных диаграмм один из векторов обычно совмещают с осью x , а другие размещают по одну или другую сторону согласно сдвигу фаз. Сложение векторов осуществляется по правилу параллелограмма или по правилу многоугольника.
Вопросы для самоконтроля
1. Что называется действующим значением переменного тока?
2. Напишите формулу, показывающую связь действующего значения переменного тока с его амплитудой.
Калькулятор действующего значения тока или напряжения
Переменный ток в отличии от постоянного двунаправленный, т.е. он течет сначала в одном направлении, а потом — в противоположном. Переменные токи вызывают и переменную разность потенциалов (переменное напряжение) на элементах электрической цепи. При этом могут быть разными не только временные характеристики, но и закон изменения (синусоидальный, пилообразный, прямоугольный и т.д.). Во многих случаях переменная составляющая напряжения или тока накладывается на ее постоянную составляющую, поэтому наиболее целесообразно оценивать величину тока по той работе, которую он совершает. Действующим значением переменного тока называется численное значение такого постоянного тока, который за время, равное одному периоду, выделяет в сопротивлении такое же количество тепла, что и ток переменный. В данном калькуляторе рассматривается только синусоидальный закон изменения тока или напряжения. Все измерительные приборы по умолчанию измеряют действующее значение. Для измерения амплитудного или пикового значения как правило используется отдельный режим. В обычной розетке переменное напряжение значением 220 вольт и указанно именно действующее значение, а амплитудное будет больше.

Um — Амплитудное значение напряжения.
Под амплитудным или пиковым напряжением подразумевают максимальный показатель U за один период синусоиды. Для измерения данного параметра обычно используют вольтметр импульсного типа или осциллограф.
Действующие значения тока и напряжения

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?
При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.
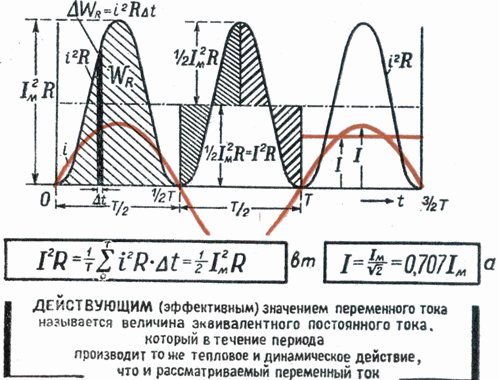
Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.
Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

Мощность Р постоянного тока I , проходящего через сопротивление r , будет Р = Р 2 r .
Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от ( Im х sin ω t ) 2 х r за то же время.
Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,
Величина I называется действующим значением переменного тока.
Среднее значение i2 при переменном токе определим следующим образом.
Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.
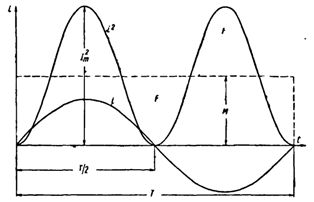
Действующее значение переменного тока
Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (- i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины.
Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно 1/2I 2 m . Следовательно, М = 1/2I 2 m
Так как действующее значение I переменного тока равно I = √ M , то окончательно I = Im / √ 2
Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:
U = Um / √ 2 E= Em / √ 2
Действующие значения переменных величин обозначаются прописными буквами без индексов ( I , U, Е).
На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.
При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого расположение векторов на диаграмме не изменяется.
Телеграмм канал для тех, кто каждый день хочет узнавать новое и интересное: Школа для электрика
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Не пропустите обновления, подпишитесь на наши соцсети:
Действующие значения тока, э.Д.С., напряжения
Действующим значением переменного тока называется такой постоянный ток, который на одном и том же резисторе сопротивлением R за то же время выделяет столько же тепла, что и данный переменный ток.
Он определяется следующим образом (как среднеквадратичное значение тока за период):
Проинтегрировав это выражение, получим
Аналогично, действующие значения э.д.с. и напряжения:
E = 0,707Em, U = 0,707Um
Im = I, Em = E, Um = U
Если периодическая величина изменяется не по закону синуса, а по какому-то другому закону, это соотношение будет другим.
В большинстве электроизмерительных приборов, измеряющих ток и напряжение, используется принцип теплового, или электродинамического эффекта. Поэтому они всегда показывают действующее значение, зная которое, можно вычислить амплитуду.
Рассмотрим следующие примеры.
В цепи, показанной на рисунке, протекает ток, мгновенное значение которого равно . Найти показание амперметра.
В цепи, показанной на рисунке, показание вольтметра равно 200В. Какое напряжение действует на изоляцию проводов?
Вольтметр показывает действующее значение напряжения.
Среднее значение тока, э.д.с., напряжения
В некоторых случаях необходимо знать среднее (то есть среднеарифметическое значение) переменного тока за половину периода, в течение которого его знак не меняется:
Проинтегрировав это выражение, получаем
Аналогично для э.д.с. и напряжения:
Eср = 0,637Em, Uср = 0,637Um.
Отношение действующего значения к среднему называют коэффициентом формы:
Для синусоидальной величины, например, тока kf = 1,11.
Для треугольной формы кривой kf = 1,15, для прямоугольной – kf = 1,0.
Формы представления электрических величин
При исследовании процессов в цепях переменного тока часто возникает необходимость суммирования нескольких однородных синусоидально изменяющихся величин одной и той же частоты, но имеющих разные амплитуды и начальные фазы.
Задачи такого рода можно решать графически в виде временных диаграмм, вращающихся векторов (или метода векторных диаграмм) и аналитически с помощью комплексных чисел.
Геометрический смысл формулы и ее параметров раскрывает временная диаграмма (справа).
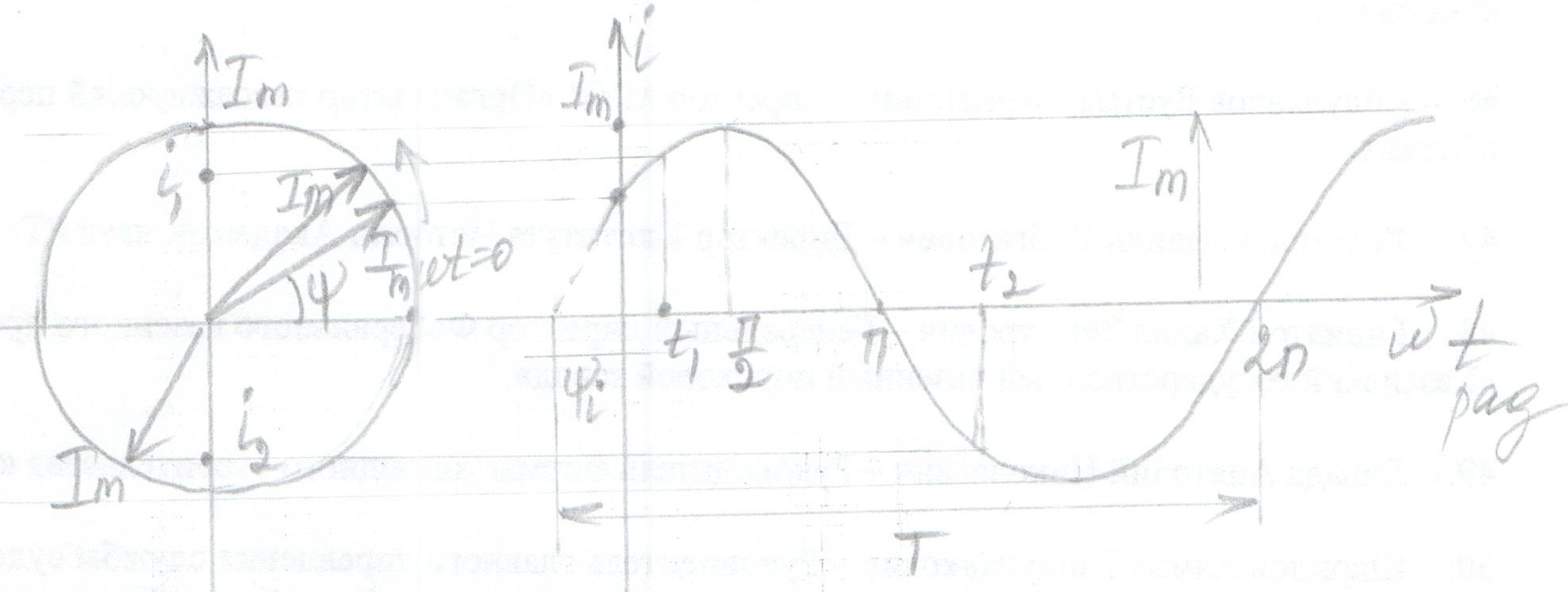
Переход от временной диаграммы к вращающимся векторам для различных моментов времени показан на рисунках а и б.
Предположим, вектор длиной Im вращается с постоянной угловой частотой ω. За положительное направление принимается направление против часовой стрелки. Проекция вращающегося вектора на ось ординат определяет мгновенное значение синусоидального тока.
Первоначальное положение вектора определяется углом ψ (начальной фазой).
Таким образом, каждой синусоидальной величине можно поставить в соответствие свой вращающийся вектор.
При действиях с несколькими синусоидами получаем несколько векторов, действия над которыми заменяют действия над синусоидальными токами или напряжениями.
Векторы-амплитуды вращаются с одинаковой скоростью, так как частота всех токов и напряжений одна, а значит, относительно друг друга они неподвижны.
Поэтому, когда диаграммы используются для сложения действующих величин напряжений и токов, то векторы не вращают.
Векторные диаграммы бывают двух типов:
Лучевой диаграммой называется диаграмма, в которой все векторы напряжений и токов цепи строят из одной точки.
Топографической диаграммой называется диаграмма, на которой векторы напряжений пристраиваются друг к другу в том же порядке, в котором они действуют в электрической цепи.
Чаще применяются топографические диаграммы.
Таким образом, векторной диаграммой называется совокупность векторов, характеризующих процесс в электрической цепи.
Метод комплексных чисел
Аналитический метод, его еще называют символическим или методом комплексных чисел, широко применяется при расчете электрических цепей переменного тока. Этот метод основан на замене геометрического сложения векторов алгебраическим сложением комплексных чисел, изображающих эти вектора.
Этот метод позволяет применять законы Ома и правила Кирхгофа для расчета цепей переменного тока с учетом специфики оперирования комплексными числами и получать более точные результаты.
Число вида , где а и b – любые действительные числа, j – мнимая единица, называется комплексным числом в алгебраической форме.
– комплексное число. Оно обозначается точкой над символом или подчеркивается внизу: ;
а – действительная (реальная) часть комплексного числа: ;
b – мнимая часть комплексного числа: ;
j – мнимая единица, или оператор поворота на 90º в положительную стороны (против часовой стрелки): или .
Два комплексных числа и называются сопряженными комплексными числами.
Используя эти соотношения, можно представить комплексное число в тригонометрической форме записи:
На основании формулы Эйлера можно записать комплексное число в показательной форме:
где jψ – поворотный множитель.
Поворотный множитель показывает, что вектор повернут относительно действительной оси на угол ψ. Отсчет угла ψ ведется от действительной оси против часовой стрелки.
Модуль комплексного числа : , обозначается или просто с.
Аргумент комплексного (равен начальной фазе): .

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое можно записать в алгебраической, тригонометрической или показательной форме.
Действия над комплексными числами
Сложение и вычитание. Эти действия удобнее производить над числами в алгебраической форме записи:
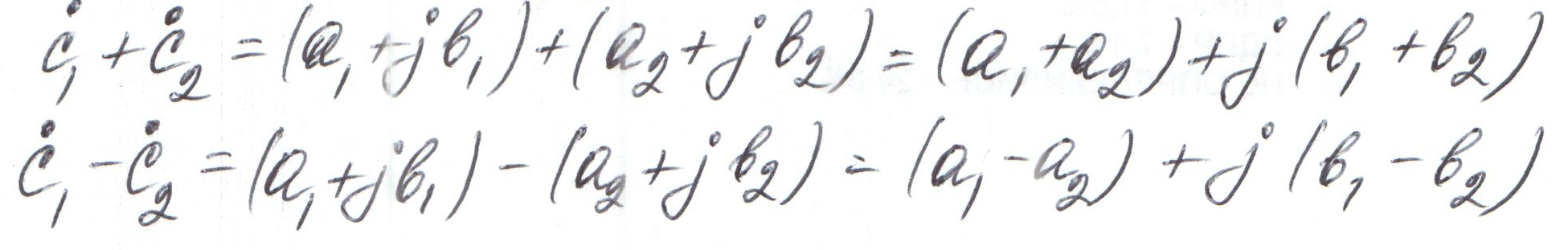
Умножение и деление удобнее производить в показательной форме:
Дан прямоугольный импульс:
- амплитуда Im = 15 А
- длительность импульса ти = 2 мс
- период Т = 10 мс
Найдем коэффициент заполнения:
D = ти / T = 2 / 10 = 0.2
По формуле для импульса:
I = Im √D = 15 √0.2 = 6.71 А
В общем случае действующее значение вычисляется по интегралу:
Где i(t) — мгновенное значение тока.
Действующему значению равно:
- Показание вольтметров и амперметров в цепях переменного тока
- Значение сетевого напряжения 220 В
Физический смысл действующих значений силы тока и напряжения
Действующие значения показывают силу тока и напряжения, эквивалентную по тепловому эффекту в цепи. Например, действующее напряжение 220 В дает такой же нагрев прибора, как и 220 В постоянного тока.
Действующее и среднее значение переменного тока




Определение 1
Действующее или эффективное значение переменного тока – это значение переменного электрического тока равное величине постоянного тока, который проделает такую же работу, сопровождающуюся тепловым эффектом или электродинамическим эффектом, что и рассматриваемый переменный ток за время равное одному периоду переменного тока.
К основным характеристикам переменного тока относятся:
- Амплитуда, являющаяся максимальным значением периодически изменяющегося тока.
- Период, который является временем, в течении которого электрическим током совершается полный цикл изменений, после чего они повторяются в той же последовательности.
- Частота, которая обратна периоду, то есть показывает количество завершенных циклов изменений за единицу времени.
- Мгновенное значение, являющееся значением переменного тока в конкретный момент времени.
- Угловая скорость или угловая частота, которая характеризуется углом поворота рамки за единицу времени.
Получи помощь с рефератом от ИИ-шки
ИИ ответит за 2 минуты
В современной литературе обычно используется математическое определение действующего значения переменного тока, которое звучит следующим образом: действующее значение переменного тока — среднеквадратичное значение переменного тока. Таким образом эта величина рассчитывается по следующей формуле:
Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ
Существует пять типичных случаев переменного электрического тока:
- Синусоида.
- Прямоугольная форма.
- Треугольная форма.
- Трапециевидная форма.
- Дугообразная форма.
Для синусоидального тока формула для расчета действующего значения выглядит следующим образом:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
Начинай год правильно
Выигрывай призы на сумму 400 000 ₽
где Im — амплитудное значение тока.
Для электрического тока, который имеет форму однополярного прямоугольного импульса используется следующая формула для расчета действующего значения.
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
где D — коэффициент заполнения.
Если коэффициент заполнения равен 0,5, то есть ток имеет форму однополярного меандра, то формула выглядит так:
$I = Im* √0.5 = 0.707*Im$
В том случае, когда у тока форма двуxполярного меандра, то:
Для токов пилообразной и треугольной формы расчет действующего значения осуществляется по формуле:
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
Посредством разбивки периода на отрезки действия максимального значения, положительного фронта и отрицательного фронта, получается формула для расчета действующего значения переменного тока трапециевидной формы:
Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ
где: t1, t2, t3 — соответственно продолжительность положительного фронта, действия максимального значения и отрицательного фронта; Т — длительность полного периода.
Для тока, который имеет форму дуги или половины окружности, формула для расчета действующего значения имеет следующий вид:
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Для измерения тока в цепях переменного тока большинство электроизмерительных приборов, таких как вольтметры и амперметры, градуируются таким образом, чтобы показания соответствовали эффективному значению переменного тока или напряжения.
Среднее значение переменного тока. Коэффициенты амплитуды и формы
Определение 2
Среднее значение переменного тока – это значение переменного тока равное величине постоянного тока, при котором через поперечное сечение проводника проходит такое же количество электричества, что и в случае переменного тока.
Среднее значение переменного тока эквивалентно постоянному по величине электричества, которое проходит через поперечное сечение проводника за определенный промежуток времени. если электрический ток изменяется согласно синусоидальному закону, то за пол через поперечное сечение проводника проходит определенное количество электричества и в определенном направлении. Таким образом его среднее значение за один период равно нулю:
Поэтому в данном случае среднее значение переменного синусоидального тока определяется за половину периода, и формула выглядит следующим образом:
где: Q — количество электричества; Т — длительность периода.
Рассмотрим рисунок, который представлен ниже.
Рисунок 7. Переменный ток. Автор24 — интернет-биржа студенческих работ
В общем виде значение переменного тока рассчитывается по формуле:
Отсюда получается, что
Таким образом среднее значение синусоидального переменного тока за половину период и с начальной фазой равной нулю на представленном выше рисунке рассчитывается по формуле:
Рисунок 8. Формула. Автор24 — интернет-биржа студенческих работ
Где: w — угловая скорость; $Т = 1/f; w = 2*п*f; п = 3,14; f $- частота электрического тока.
Графически среднее значение синусоидального переменного тока является высотой прямоугольника, основание которого равняется половине периода, а площадь ограниченна кривой электрического тока и осью абсцисс за половину периода.
Средним значением переменной величины является постоянная составляющая данной величины. Поэтому, чтобы рассчитать среднее значение переменного напряжения и электродвижущей силы можно использовать формулы:
где: Um — амплитудное значение напряжения; Еm — амплитудное значение электродвижущей силы.
Отклонения кривых электрического тока от синусоиды характеризуется коэффициентами формы и амплитуды. Отношением действующего значения переменной величины к ее среднему значению определяется коэффициент формы, то есть:
Коэффициент формы должен учитываться в процессе проектирования и изучения выпрямительных устройств и электрических машин. Для синусоиды коэффициент формы рассчитывается следующим образом:
$Кф = (Im*п) / (√2*2*Im) = 1.11$
Чтобы рассчитать коэффициент амплитуды, используется формула:
где I — действующее значение переменного тока.
Для синусоидальной величины формула имеет следующий вид:
$Ка = (I*√2) / I = /2 = 1,41$
Чем больше значение коэффициентов амплитуды и формы отличаются от иx значения для синусоидальных величин, тем больше кривая электрического тока отличается от синусоиды.
Электротехника ТОЭ
Лекции и задачи по ТОЭ. На сайте представлен лекционный материал для изучения теоретических основ электротехники и видеоуроки по всем темам. Так же тут можно заказать решение задач, курсовых, расчетных, контрольных и домашних работ. Онлайн помощь на экзамене, контрольной. Решение тестов, занятия по скайпу и др. В ближайшее время на сайт будут добавлены готовые работы на разные темы ТОЭ, ТАУ и другим дисциплинам.
Теория / 4.3. Действующее и среднее значения переменного тока
Основной задачей расчета электрической цепи является определение тока. В цепях постоянного тока, если нет регулирующих устройств, ток остается неизменным и его легко рассчитать или измерить. В цепях переменного тока ток непрерывно меняется по величине и по направлению. Если, допустим, что каким-либо путем нам удалось определить одно мгновенное значение тока, то это не даст оценки действия всех остальных значений.
Поэтому переменный ток оценивается по его действию, которое эквивалентно действию некоторого постоянного тока. В качестве критерия такой эквивалентности принято считать тепловое действие тока.
Действующее значение переменного тока численно равно такому постоянному току, который в элементе цепи за время, равное периоду Т, выделяет такое же количество тепла, какое в том же элементе за то же время при тех же условиях выделяет переменный ток.
Определим количество тепла, которое выделяется за период Т постоянным током.
По закону Джоуля – Ленца:
Для переменного тока
По определению количество тепла, выделяемое постоянным и переменным токами, должно быть одинаково.
Тогда действующее значение тока определится выражением
Полученное выражение справедливо для любого переменного тока независимо от его формы.
Определим действующее значение синусоидального тока. Представим мгновенное значение тока в виде
тогда будет справедливо соотношение:
Используя правила тригонометрических преобразований, выразим
Действующее значение синусоидального тока в корень из 2 раз меньше его амплитудного значения.
То же самое можно сказать о напряжении и ЭДС:
Действующие значения токов, напряжений и ЭДС обозначаются прописной буквой без индекса. Все расчеты в цепях переменного тока выполняются для действующих значений токов, напряжений и ЭДС.
Действующее значение переменного тока можно измерить приборами любой системы, кроме магнитоэлектрической.
Отношение амплитуды к действующему значению тока называется коэффициентом амплитуды.
Для синусоидальных токов коэффициент амплитуды всегда равен корню из 2.
В ряде случаев при анализе электрических цепей переменного тока необходимо определить среднее значение переменного тока.
Средним значением переменного тока называется среднее арифметическое из всех мгновенных значений за половину периода.
Для синусоидальных величин среднее значение всегда оценивается за половину периода, так как мгновенные значения полпериода положительны, а полпериода – отрицательны, в результате среднее значение за период равно нулю.
Найдем среднее значение переменного тока:
Отношение действующего значения к среднему называется коэффициентом формы кривой.
Подставив эти значения в формулу коэффициента формы, получим для синусоидального тока
Таким образом, действующие значения тока, напряжения и э.д.с. связаны со средними значениями соотношениями:
Величины, характеризующие переменный ток
В промышленных генераторах используют много пар магнитных полюсов. От их количества прямо пропорционально зависит значение частоты переменного тока. В различных государствах пользуются переменным током разной стандартной частоты: в Соединённых Штатах Америки — (60) Гц, в Российской Федерации — (50) Гц. Это значит, что происходит изменение направления электрического тока за (1) секунду (50) раз в каждую сторону.
Сила тока, получаемого с помощью такого генератора, изменяется с течением времени по гармоническому закону.

По графику силы тока видно, что она меняется от максимального ( амплитудного ) значения до нуля и обратно на протяжении одного периода.
При вычислении работы и мощности переменного тока необходимо учитывать гармоническую зависимость от времени значений силы тока (I(t)) и напряжения (U(t)), поэтому вводятся термины « мгновенная мощность (P(t))» и « средняя мощность (P)».
Для того чтобы формула средней мощности переменного тока (при наличии в электрическом контуре только сопротивления) не отличалась от формулы мощности постоянного тока ((P = UI)), вводятся термины « действующее значение силы тока » и « действующее значение напряжения ».




