Логическая константа, логическая переменная, логическая операция, логическая функция, эквивалентные преобразования логических выражений, таблицы истинности логических операций и логических выражений.
Основные логические операции и законы логики рассматривались в билетах № 7 и 8 (вопросы № 2).
Логическая, константа имеет одно из значений — ИСТИНА (TRUE, 1) или ЛОЖЬ (FALSE, 0). Соответственно, логическая переменная может принимать одно из вышеуказанных значений.
Логическое выражение — это выражение, состоящее из логических операндов, соединенных с помощью логических операций. В качестве логических операндов могут выступать логические константы, переменные, а также отношения (сравнения) между двумя не обязательно логическими величинами. Логические выражения могут принимать одно из двух значений: ИСТИНА (TRUE или 1) или ЛОЖЬ (FALSE или 0). Отношение — это два выражения некоторого одного и того же типа, соединенных операцией отношения («>», «»). Обычно в языках программирования операции отношения определены для величин числовых, символьных, логических, строковых типов.
В определенных случаях сложные логические выражения могут быть заменены более простыми путем равносильных преобразований. Вообще два логических выражения являются равносильными, если имеют одинаковые таблицы истинности.
При такого рода преобразованиях применяются законы алгебры логики (билет № 8, вопрос № 2). Примеры см. в «Информатике» № 17, с. 3 — 7.
Равносильные преобразования логических выражений необходимы, например, при конструировании логических схем с целью минимизации количества логических элементов, их составляющих.
Таблицы истинности можно составлять вручную или использовать программирование (заметим только, что для каждого выражения это будет своя программа). Примеры там же.
В языках программирования есть некоторое количество логических функций, которые позволяют анализировать определенные ситуации. Например, eof (f) в языке Паскаль возвращает true, если достигнут конец файла f, и false в противном случае.
При реализации некоторых программ удобно использовать функции, которые имеют логическое значение. Обычно они используются для того, чтобы на некоторый вопрос получить ответ «да» или «нет».
Например, следующая функция возвращает true, если ее натуральный аргумент — простое число, и false — в противном случае:
Function Simple (Pr : Integer) : Boolean; Var I : Integer; LogPer : Boolean; Begin
1: Simple := false;
значение TRUE, если число Pr
LogPer := (Pr Mod I = 0); I := I + 1
Until (I > Pr Div 2 + 1) Or (LogPer);
(цикл завершаем в том случае, когда
счетчик становится больше половины
данного числа или обнаруживаем, что
Simple := Not LogPer
Примечание для учителей
Алгебра логики: Логические переменные и логические функции. Центр онлайн-обучения «Фоксфорд»
Вопрос билета целесообразно сформулировать так, как он формулировался ранее: «Логические выражения и их преобразования. Таблицы истинности». В нынешней формулировке он является некорректным.
Примечание для учеников
Понимание сущности алгебры логики, умение правильно составлять и преобразовывать логические выражения способно существенно помочь при изучении программирования и составлении программ.
Ссылка на материалы вопроса
«Информатика» № 17, с. 3 — 7.
3. Задача. Разработка алгоритма (программы) на обработку данных строкового типа
Принципы составления задания
При составлении задания целесообразно учесть, что в разных, языках программирования строки реализованы по-разному. В некоторых (например, Паскаль, C/C++) строки можно интерпретировать и как массив символов, и как единое целое, в других (Бейсик) только как единое целое. Поэтому специфика изучаемого учащимися языка должна быть учтена в экзаменационном задании.
Примеры разобранных задач с решением можно найти в «Информатике» № 17, с. 3— 7.
Работа со строковым типом данных в языке Паскаль описана здесь: http://comp-science.narod.ru/Prog/ String.htm.
Задачи для экзамена можно взять из таких задачников:
1) Информатика. Задачник-практикум в 2 т. / Под ред. И.Г. Семакина, Е.К. Хеннера. Т. 1, 2. М.: Лаборатория Базовых Знаний, 1999.
2) Шауцукоба Л.З. Информатика: Учебное пособие для 10—11-х классов общеобразовательных учреждений, 2-е изд., дораб. М.: Просвещение, 2002, 416 с.
3) Златополъский Д.Л1 Я иду на урок информатики. Задачи по программированию. 7—11-е классы: Книга для учителя. М.: Издательство «Первое сентября», 2002, 208 с.
1. Основные этапы в информационном развитии общества. Основные черты информационного общества. Информационные ресурсы.
2. Количество информации как мера уменьшения неопределенности знаний. Содержательный подход к измерению информации.
I 3. Практическое задание. Разработка мультиме-| дийной презентации на свободную тему
1. Основные этапы в информационном развитии общества. Основные черты информационного общества. Информационные ресурсы
Информационное развитие, информационная технология, информационное общество, информационный ресурс.
Информационное развитие общества прошло несколько основных этапов, каждый из которых был связан с информационной революцией — преобразо-
ванием общественных отношений из-за кардинальных изменений в сфере обработки информации.
Первый этап связан с изобретением письменности, которое создало возможность передачи знаний от поколения к поколениям.
Второй этап начался изобретением в середине XVI в. книгопечатания, которое радикально изменило индустриальное общество, культуру, организацию деятельности.
Третий этап (конец XIX в.) обусловлен изобретением электричества, благодаря которому появились телеграф, телефон, радио, позволяющие оперативно передавать и накапливать информацию в любом объеме.
Четвертый этап, начавшийся в 70-е гг. XX в., связан с изобретением микропроцессорной технологии. На микропроцессорах и интегральных схемах создаются компьютеры, компьютерные сети, системы передачи данных (информационные коммуникации).
Последняя информационная революция выдвинула на первый план новую отрасль — информационную индустрию, связанную с производством технических средств, методов, технологий для производства новых знаний. Важнейшими составляющими информационной индустрии являются все виды информационных технологий — процессов, использующих совокупность средств и методов сбора, обработки и передачи данных (первичной информации) для получения информации нового качества о состоянии объекта, процесса или явления.
Развитие информационной индустрии послужило толчком к формированию и развитию общества, построенного на использовании различной информации и получившего название информационного общества. Это общество имеет следующие основные черты:
• большая часть населения развитых стран занята информационной деятельностью;
• одной из главных социальных ценностей, объединяющих общество, главным продуктом производства и основным товаром является информация;
• с помощью средств информатики реализуется свободный доступ каждого человека к информационным ресурсам всей цивилизации;
• власть в обществе принадлежит информационной элите;
• классовая структура общества лишается смысла и постепенно уступает место элитарно-массовой структуре.
Понятие «информационного ресурса общества» является одним из ключевых понятий социальной информатики. Его появление было обусловлено растущей зависимостью промышленно развитых стран от источников информации (технической, экономической, политической, военной), а также от уровня развития и эффективности использования средств передачи и переработки информации.
Понятие информационного ресурса находится в стадии формирования, трудность его однозначного определения связана с неоднозначностью и сложностью таких понятий, как «знания», «информация», «данные» и т.д.
Информационный ресурс общества может быть определен как накопленные в обществе знания, подготовленные для целесообразного социального использования.
С понятием «информационный ресурс» тесно связано понятие «информационный потенциал общества» — это информационный ресурс общества в единстве со средствами, методами и условиями, позволяющими его активизировать и эффективно использовать.
Привести примеры накопленных знаний, которые включаются и не включаются в информационный ресурс.
Ссылка на материалы вопроса
1. Шауцукова Л.З. Информатика: Учебное пособие для 10—11-х классов общеобразовательных учреждений. М.: Просвещение, 2002, 416 с.
2. Ершова Т.Е. Вестник РФФИ № 3, 1999.
2. Количество информации как мера уменьшения неопределенности знаний. Содержательный подход к измерению информации
Информация, знания, сообщение, содержательный подход.
Понятие «информация», обозначающее предмет информатики, определяется с помощью перечисления отличительных свойств и действий, которые с информацией можно совершать, а также указания того, что является носителем информации. Главными свойствами информации являются передаваемость, хранимость, преобразуемость. К ним часто добавляют атрибуты: достоверность, полезность, значимость и т.д. Информацию можно создавать, воспринимать, запоминать, распространять, обрабатывать, разрушать, измерять и т.д. Носителями информации являются сообщения, т.е. последовательность знаков, принадлежащих некоторой знаковой системе.
Прообразом понятия «информация» является то, что в быту называют знаниями, т.е. сведениями об окружающем нас мире в их взаимной связи. Поэтому, когда говорят о содержательной стороне информации, обычно имеют в виду именно знания. Измерение знаний оказывается очень непростой задачей. Так, если сообщение о новом научном открытии написано на неизвестном нам языке, мы говорим, что не получили никакой информации. Если сообщение написано на известном языке, но касается незнакомой области науки или производства, мы также делаем вывод о том, что для нас сообщение не информативно. Вывод об отсутствии информации в понятном сообщении делается и в том случае, когда знания, в нем содержащиеся, для нас уже известны или требуют для своего восприятия большего запаса знаний, чем тот, что у нас имеется. Таким образом, оценка присутствия знаний в сообщении определяется приемником сообщения по таким атрибутам, как понятность, новизна и полезность по отношению к сумме знаний, которой он обладает. Вопрос о количестве информации, т.е. о сравнении информативных сообщений, при этом не возникает.
Рассмотрим теперь подход, в котором приобретают смысл утверждения о том, много или мало информации содержится в данном сообщении, полученном данным приемником. Известно, что на базе имеющихся знаний можно прогнозировать последствия различных событий в окружающем нас мире. Именно так и происходит общение человека с его окружением. Мы «задаем вопросы» и получаем в ответ сообщения, которые в той или иной степени подтверждают или отрицают наши прогнозы относительно последствий тех или иных событий. Если сообщение подтверждает наиболее ожидаемый прогноз, мы говорим, что оно содержит меньше информации, чем сообщение с подтверждением наименее ожидаемого прогноза. На математическом языке эту ситуацию можно описать словами: сообщение о реализации более вероятного предполагаемого результата содержит меньше информации, чем сообщение о реализации менее вероятного результата. Поскольку использование прогнозирования означает неполноту или неопределенность наших знаний, можно сказать, что информация, содержащаяся в сообщениях подобного типа, уменьшает неопределенность наших знаний. Этот подход, допускающий сравнение сообщений по их информативности, в качестве следующего шага позволяет определить количество информации с помощью соглашения о том, как изменяется неопределенность наших знаний при получении сообщения с определенной информацией. Принято считать, что сообщение, уменьшающее неопределенность наших знаний в два раза, содержит количество информации, принимаемое за единицу ее измерения. Эта единица измерения получила название бит. Если говорить о содержании, то это сообщение с одним из двух альтернативных равновероятных ответов на сформулированный специальным образом вопрос. Например, вопрос о том, мужчина или женщина совершенно незнакомый человек по фамилии Тарасюк, допускает два альтернативных равновероятных ответа, а значит, получая любой из них, мы получаем информацию в количестве 1 бит.
Чтобы воспользоваться этой единицей измерения для определения количества информации в произвольном сообщении, нужно представить его как ответ на вопрос, который допускает замену серией специальных вопросов с ответами, содержащими 1 бит информации, подобно алгоритму поиска корней функции с помощью метода деления отрезка пополам. Например, получив сообщение в виде черно-белого изображения, мы можем представить его как ответ на вопрос о распределении черных и белых точек на заданной площади. Этот вопрос допускает замену серией вопросов о том, каков цвет точки, находящейся в заданной позиции. Ответ на каждый из них содержит 1 бит информации по определению, так что полное количество информации равно количеству точек, образующих данное изображение.
Применение этой схемы для определения количества информации в цветном изображении сразу наталкивается на непреодолимые трудности, связанные с необходимостью учета законов композиции, индивидуальности художника и т.д. Ситуация становится еще более запутанной, если приемник обладает какими-либо особенностями восприятия изображений. Еще больше неразрешимых проблем в рамках содержательного подхода возникает при попытке найти количество информации в битах, содержащееся в каком-либо литературном произведении, и т.д.
Подводя итог, можно сделать неутешительный вывод о том, что в рамках содержательного подхода к определению количества информации, как количества знаний в сообщении, с помощью указанной единицы измерения в данном случае не представляется возможным.
Ссылка на материалы вопроса
1. Семакин И., Залогова А., Русаков С., Шестакова А. Базовый курс для 7—9-х классов. М.: Лаборатория базовых знаний, 2001, 384 с.
2. Шауцукова А.З. Информатика: Учебное пособие для 10—11-х классов общеобразовательных учреждений. М.: Просвещение, 2002, 416 с.
3. Разработка мультимедийной презентации на свободную тему
Принципы составления задания
Мультимедийная презентация предполагает одновременное использование чисел, текстов, графики, анимации, видео, звука. Разработка полноценной презентации за время экзамена вряд ли возможна. Поэтому следует ограничиться текстом, графикой и анимацией, что позволяет использовать MS Power Point в стандартной конфигурации. Тексты размещаются на слайдах как объекты «Надпись». Графические изображения создаются с помощью панели «Рисование» или выбираются из стандартной коллекции рисунков. Анимация осуществляется с помощью встроенных эффектов и касается не только объектов, расположенных на слайдах, но и процесса перехода от одного слайда к другому. В случае затруднений в выборе темы презентации можно предложить следующие:
1. Архитектура современного компьютера (двухслай-довая презентация; первый слайд представляет основные элементы компьютерной системы — процессор, оперативную память, винчестер, видеоадаптер, клавиатуру и т.д.; второй —их соединение).
2. Основные алгоритмические структуры (двухслай-довая презентация; первый слайд представляет структуры «следование» и «ветвление»; второй циклы).
Для повышения оценки можно предложить разместить на слайдах элементы управления.
Угринович Н.Д. Информатика и информационные технологии. Учебное пособие для 10—11-х классов. Углубленный курс. М.: Лаборатория Базовых Знаний, 2000, 440 с.
I 1. Этические и правовые аспекты информационной деятельности. Правовая охрана программ и | данных.
I 2. Основные способы защиты информации на I локальном компьютере и в компьютерных сетях.
Логическая переменная – это переменная, принимающая состояние, соответствующая одному из двух элементов ансамбля E.
В качестве элементов ансамбля E могут быть использованы различные понятия. Например: 0 или 1, истина или ложь, открыто или закрыто, и так далее. На практике говорят, что логическая переменная может принимать два состояния или две величины: 0 и 1.
Над логическими переменными может быть осуществлен некоторый набор операций точно так же как и в классической алгебре над числами.
Однако необходимо принимать во внимание, что в Булевой алгебре 0 и 1 не должны рассматриваться как числа классической алгебры, а только как символы, соответствующие одному из состояний.
1.2. Логические функции
Логическая функция от n переменных x1, x2, …, xn – это функция, которая может принимать только два значения 0 или 1.
Каждая переменная может принимать только два значения. Следовательно имеется 2 n возможных комбинаций n переменных.
Логическая функция будет определена, если известно ее значение для каждой из 2 n возможных комбинаций. Она может быть представлена с помощью соответствующей таблицы истинности.
Рассмотрим, например функцию трех переменных f(x,y,z). Функция f(x,y,z) будет определена, если будут заданы ее значения (0 или 1) для каждой из восьми комбинаций таблицы:
III Бесконечный цикл while
Заметим также, что в примерах выше условие цикла while рано или поздно становилось ложным, и цикл завершал свою работу. Если же написать такое условие, которое всегда будет истинно, то можно получить бесконечный цикл while , который будет выполняться до тех пор, пока у компьютера хватит ресурсов. Поэтому при работе с циклом while всегда необходимо проверять, что он не будет бесконечным. Но иногда специально нужно использовать именно бесконечный цикл while . Тогда возникает потребность в команде для принудительного выхода из цикла и его завершения. Такая команда есть, и она абсолютна безвредна для программного кода. Это команда break; . Она принудительно завершает любой цикл (и цикл for в том числе), когда это необходимо по соображениям алгоритма. Рассмотрим следующий код:
int k = 0; while(2 > 1)< printf(«%d) Do something. n», k + 1); if (k >= 15) < break; >else < k++; >>
При его запуске программа выведет в консоли:
1) Do something. 2) Do something. 3) Do something. 4) Do something. 5) Do something. 6) Do something. 7) Do something. 8) Do something. 9) Do something. 10) Do something. 11) Do something. 12) Do something. 13) Do something. 14) Do something. 15) Do something. 16) Do something.
Не трудно заметить, что в этом случае ограничителем является не убывающее значение переменной, находящейся внутри условия цикла while , а возрастающее значение сторонней переменной. Цикл while является бесконечным, а его завершение происходит по команде break; после достижения значения переменной k числа 15. Так как изначально значение переменной k было 0 , то в консоль выписалось 16 строк (чисел от 0 до 15 — 16 штук). Бесконечный цикл while обычно создают при помощи логических переменных:
while (true)< // делаем что-нибудь >
IV Подсчёт суммы цифр числа
Подсчёт суммы цифр числа является популярной и распространённой задачей. А также данная задача явно демонстрирует преимущество цикла while над циклом for . Как мы уже знаем, чтобы вычислить последнюю цифру числа, нужно взять остаток при делении этого числа на 10. А чтобы получить вторую справа цифру числа, нужно сначала разделить данное число на 10 в целых числах, а затем снова взять остаток при делении на 10. Таким образом, мы получаем явный цикл, состоящий из команд взятия остатка при делении на 10 и делении на 10 в целых числах. Но загвоздкой и невозможностью применить цикл for является тот факт, что мы не можем жестко задать, сколько раз необходимо повторять вышеуказанные команды, так как числа могут быть совершенно различной размерности. Например, для трехзначных чисел необходимо выполнить данные команды 3 раза, а для шестизначных — 6 раз. Поэтому цикл for в данной задаче неприменим. А вот цикл while справится с подсчётом суммы цифр на ура. Заметим, что команды взятия остатка при делении на 10 и делении на 10 в целых числах необходимо выполнять до тех пор, пока число не станет нулём. И таким образом получается явная конструкция с использованием цикла while :
while (x > 0)< // пока переменная х больше нуля s += x % 10; // прибавляем к переменной s последнюю цифру числа х x /= 10; // делим число х на 10 в целых числах >
Что такое логическая переменная
В прошлом задании мы работали с числовыми типами переменных и учили арифметику, теперь познакомимся с логическим типом переменных, который называется Boolean . Переменные этого типа имеют всего два значения — true и false (соответственно, «истина» и «ложь»). Подобно числовым переменным им можно присваивать значения при помощи оператора присваивания. При этом необходимо строго соблюдать правило совместимости типов. То есть, логическим переменным нельзя присваивать числовые значения, а числовым — логические. Так же можно выводить значения логических переменных на экран, а вот вводить их с клавиатуры нельзя!
В языке Pascal определены `6` операций сравнения, результатом которых является логическое значение:
2) «больше или равно» (>=)
4) «меньше или равно» (<=)
Например, операция `5>2` всегда выдаст значение true , а операция `x<>3` выдаст значение true , если переменная `x` имеет любое значение, кроме `3`.
Сравнивать можно не только числа (причём как целые, так и вещественные), но и логические значения. При этом считается, что значение true больше , чем значение false.
При выполнении сравнений также необходимо соблюдать совместимость типов. То есть, можно сравнивать число с числом или логическое значение с логическим значением, но нельзя сравнивать число с логическим значением. Такое сравнение выдаст ошибку.
Помимо операций сравнения ещё существуют и логические операции:
1) and (конъюнкция, логическое умножение, операция «И»)
2) or (дизъюнкция, логическое сложение, операция «ИЛИ»)
3) not (отрицание, инверсия)
4) xor (строгая дизъюнкция, исключающее «ИЛИ», сложение по модулю `2`).
В скобках указаны возможные названия данных операций в алгебре логики.
Операнды этих операций должны быть логического типа. Результат вычислений также будет логический. При этом операции and, or, xor имеют по два операнда, а операция not — всего один, который записывается справа от названия операции. Названия логических операций являются служебными зарезервированными словами языка.
Приведём таблицы результатов логических операций для всех возможных значений операндов (в алгебре логики такие таблицы называются таблицами истинности):
Логический тип переменных.
презентация к уроку по информатике и икт (8 класс)
Презентация для урока информатики в 8 классе. В презентации дается понятие логической переменной, рассказывается об операциях сравнения и формировании простых и сложных условий. Подробно объясняются логические операции. Разбираются примеры задач на логические переменные.
| | 116.07 КБ |
Предварительный просмотр:
Подписи к слайдам:
Логический тип переменных Учитель: Н.В. Фоменко
Как компьютер принимает решение? Конечно , ему не приходится принимать решение, как человеку. Однако логики и определенности в поведении компьютера куда больше. Собственно, никаких колебаний у него и не бывает. Каждый раз, когда компьютер принимает решение, оно четко и окончательно: или да, или нет! Согласитесь, подобной решимости людям зачастую не хватает.
Попробуем разобраться с логикой компьютера Логика оперирует утверждениями. Любое утверждение может быть истинным или ложным. При решении задач требуется проверить некоторое условие, сформулированное в виде утверждения, и в зависимости от результата проверки (истинности или ложности) произвести те или иные действия. Если условие выполняется, результат будет «истина», если нет – то «ложь». Например, утверждение 4>3 – истина, а 2>3 – ложь. Такие выражения называются логическими. Для хранения результата проверки условий введен логический тип переменных – boolean . Переменные такого типа называются логическими
Логические переменные Переменные логического типа принимают всего два значения: false (ложь) и true (истина); причем они определены так, что false b, а также можно этот результат напечатать . На экран будет выведено соответственно false или true .
Операции сравнения: – больше >= – больше или равно = – равно – неравно
Задача. Проверить, является ли введенное число n четным. Пусть otvet — логическая переменная, n — целая переменная. В результате выполнения оператора присваивания otvet := n mod 2=0 переменной otvet будет присвоено значение true при любом чётном n и false в противном случае. program chetnye ; var n: integer; otvet : boolean ; begin writeln (‘ Введите исходное число’); readln (n); otvet := n mod 2=0; writeln (‘ Число ‘, n,’ является четным — ‘, otvet ) end.
Сложные условия Часто принимаемое решение зависит от результата не одного, а нескольких утверждений. Например, «Вася сегодня получит 5, если придет на урок и правильно выполнит задания», то есть нужно научиться формировать сложные условия. На Паскале сложные условия формируются из простых с помощью логических операций.
Логические операции в Паскале Логическая операция Название операции and Операция И (логическое умножение) or Операция ИЛИ (логическое сложение) not Операция НЕ Логическое отрицание (инверсия) xor Операция ЛИБО ( Исключающее ИЛИ)
Логическая операция AND Сложное выражение, составленное с помощью операции and , истинно тогда и только тогда, когда истинны все простые выражения, входящие в его состав X>3 X 3 and X 3) and (x 3 X 3) or (X 3 X 3) xor (X 3 not (X> 3) 0 1 1 0
Приоритеты 1) not 2) and 3) or, xor Это значит, что сначала выполнится операция not , за ней and и только потом – or или xor , которые имеют одинаковый приоритет На паскале недопустимо записывать сложное условие в виде двойного неравенства: 2 =2) and (x 0) and (b mod 2 <>0) А можно так: f:= ( a+b ) mod 2=0
Что такое логическая переменная
В прошлом задании мы работали с числовыми типами переменных и учили арифметику, теперь познакомимся с логическим типом переменных, который называется Boolean . Переменные этого типа имеют всего два значения — true и false (соответственно, «истина» и «ложь»). Подобно числовым переменным им можно присваивать значения при помощи оператора присваивания. При этом необходимо строго соблюдать правило совместимости типов. То есть, логическим переменным нельзя присваивать числовые значения, а числовым — логические. Так же можно выводить значения логических переменных на экран, а вот вводить их с клавиатуры нельзя!
В языке Pascal определены `6` операций сравнения, результатом которых является логическое значение:
2) «больше или равно» (>=)
4) «меньше или равно» (<=)
Например, операция `5>2` всегда выдаст значение true , а операция `x<>3` выдаст значение true , если переменная `x` имеет любое значение, кроме `3`.
Сравнивать можно не только числа (причём как целые, так и вещественные), но и логические значения. При этом считается, что значение true больше , чем значение false.
При выполнении сравнений также необходимо соблюдать совместимость типов. То есть, можно сравнивать число с числом или логическое значение с логическим значением, но нельзя сравнивать число с логическим значением. Такое сравнение выдаст ошибку.
Помимо операций сравнения ещё существуют и логические операции:
1) and (конъюнкция, логическое умножение, операция «И»)
2) or (дизъюнкция, логическое сложение, операция «ИЛИ»)
3) not (отрицание, инверсия)
4) xor (строгая дизъюнкция, исключающее «ИЛИ», сложение по модулю `2`).
В скобках указаны возможные названия данных операций в алгебре логики.
Операнды этих операций должны быть логического типа. Результат вычислений также будет логический. При этом операции and, or, xor имеют по два операнда, а операция not — всего один, который записывается справа от названия операции. Названия логических операций являются служебными зарезервированными словами языка.
Приведём таблицы результатов логических операций для всех возможных значений операндов (в алгебре логики такие таблицы называются таблицами истинности):
Логическая функция и элемент И-НЕ
Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.
Рис. 1.4. Логический элемент И-НЕ на три входа
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.
В логических выражениях применяются обозначения:
- либо
 , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
, но при этом из контекста должно быть ясно, что данное умножение именно логическое; - либо
 ;
; - либо
 ;
; - либо
 .
.
Логическая функция и элемент ИЛИ-НЕ
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а. Таблица истинности приведена на рис. 1.5,б.
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.В логических выражениях применяются обозначения:
- либо
 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое; - либо
 .
.

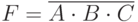 , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
, но при этом из контекста должно быть ясно, что данное умножение именно логическое;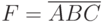 ;
; ;
; .
.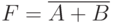 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое;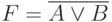 .
.


