Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10 -3 сек.
1 мкс=0,001 мс = 0,000001сек =10 -6 сек.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 10 3 Гц = 1 кГц;
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Отличие переменного и постоянного тока наглядно.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2 .

Рисунок 2. Радиан.
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2 ). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .
? = 6,28*f = 2f
Что такое частота
Производство электроэнергии в подавляющем большинстве ситуаций называют контролируемым. Эту работу проделывают генераторы, преобразующие механическую энергию ротора турбины в электрическую. Как показано на схеме, на поверхности ротора имеется обмотка из медной проволоки, поэтому он представляет собой непрерывно вращающийся электромагнит.

Схематическое изображение генератора
Во время вращения ротора, созданное вокруг него магнитное поле, наводит электрический ток. Его направление периодически изменяется на противоположное, поскольку месторасположение полюсов электромагнита чередуется после каждого оборота ротора. Соответственно, ток тоже меняет своё направление два раза за цикл вращения.
Следствием и мерой скорости этих изменений является частота, которая измеряется количеством изменений месторасположения полюсов в секунду. Единица частоты получила наименование герц и обозначается двумя буквами — Гц. Таким образом, можно сказать, что генератор, который снабжён парой магнитных полюсов, вращающихся с угловой скоростью 3000 мин -1 , будет производить ток частотой 50 Гц.
Мощность переменного тока изменяется по синусоидальному закону с чередованием положительных и отрицательных полюсов. При переходе каждого цикла из положительной области в отрицательную происходит соответствующее перемещение электронов. В конечном счете, эти циклы создают электрический нагрев или рассеивание мощности. Независимо от направления движения тока (т. е., положительного или отрицательного), если силы тока (напряжения) достаточно для удовлетворения требований электрического устройства, оно будет работать.

Синусоида переменного тока
Таким образом, количество полных циклов за секунду, когда переменный ток переходит от положительного полюса к отрицательному, называется частотой, а сам временной отрезок называется периодом. С точки зрения электрического тока частотой принято считать количество повторений синусоиды, а другими словами — это полное колебание, состоящее из положительной и отрицательной составляющих. Следовательно, частота и период связаны между собой обратно пропорциональной зависимостью:

Определение частоты
Частота и период переменного тока варьируются в зависимости от страны, причём не обязательно привязываются к местному стандарту напряжения. Например, в США, Канаде и других странах со стандартным линейным напряжением 110…120 В эталоном частоты является 60 Гц. В большинстве стран, где значения переменного напряжения равняются 220…240 В (в том числе и в нашей стране), за стандартную частоту принято 50 Гц, однако Южная Корея, Филиппины и многие страны Карибского бассейна используют 220…240 В с частотой 60 Гц. А есть ещё и Япония, где напряжение в сети достигает 100 В, но стандартная частота переменного тока в разных районах составляет 50 и 60 Гц.
Большинство электронных устройств могут работать, потребляя переменный ток, если его частота 50 или 60 Гц. Но, для электроприборов, использующих довольно мощные приводы, рассчитанные на конкретную частоту (холодильники, морозильники, стиральные и сушильные машины), разница в 10 Гц уже значительна. В первую очередь это касается устройств, включающихся периодически. Их электромоторам приходится вращаться то быстрее, то медленнее, что отрицательно сказывается на их долговечности. В таких случаях необходимо использовать преобразователи частоты или трансформаторы напряжения.

Внешний вид преобразователя частоты
Как определяется
Существует два способа установить, чему равна частота и амплитуда переменного тока — применять специальные приборы либо воспользоваться результатами расчётов.
Измерение частоты
Для измерения частоты переменного тока используется принцип механического резонанса. Он является достаточно простым, хотя и не очень точным. Основывается на том факте, что для каждого физического объекта, обладающего упругими свойствами, существует определенное значение частоты, при которой он начинает вибрировать.
Примером подобного устройства является камертон. Если по нему ударить, он будет довольно продолжительное время вибрировать со звуком, зависящим от его длины. Чем длиннее камертон, тем ниже будет резонансная частота и наоборот.
Если представить себе ряд камертонов с постепенно увеличивающимися размерами, установленными на общем основании, то это основание станет вибрировать с частотой измеряемого напряжения или тока. Для этого устройство следует снабдить электромагнитом.
Измерения частоты тока выполняются с помощью набора «камертонов», в качестве которых используются полоски листового металла. Это устройство называется частотомером вибрирующего геркона.

Схема вибрационного частотомера
Используя частотомер, можно наглядно увидеть, как концы всех полосок встряхиваются в зависимости от того, как меняется величина переменного напряжения, приложенного к катушке. Тот из лепестков, который будет ближе всего к резонансной частоте переменного тока, станет вибрировать наиболее интенсивно.
Особой точностью вибрационные частотомеры не отличаются, зато характеризуются простотой своего изготовления. Их применяют в небольших электроремонтных мастерских, а также в быту с целью калибровки частоты вращения двигателя.
Хотя подобный прибор будет иметь малую точность, этого нельзя сказать о самом принципе измерения. Заменив механический резонатор на электрический, можно получить частотомер на основе катушки индуктивности и параллельно включённого конденсатора. Вместе они образуют колебательный контур.
Один или оба компонента этого контура могут быть регулируемыми. В цепь включается измерительный блок, который показывает максимальную амплитуду напряжения на конденсаторе и катушке. Ручки регулировки предварительно откалибровываются, чтобы иметь возможность выставлять резонансную частоту для любого варианта настройки. Частота считывается после настройки устройства на максимальное показание шкалы измерителя.

Схема электрического частотомера
Фактически частотомер реализует схему настраиваемого фильтра, после чего отсчёт показаний происходит как в мостовой схеме (она вначале балансируется для условного нулевого состояния, после чего выполняется отсчёт). До тех пор, пока катушка и/или конденсатор смогут перехватывать достаточное поле магнитного или электрического рассеивания от тестируемой цепи, устройство будет сохранять свою работоспособность.
Метод не требует прямого подключения к цепи, поэтому часто применяется в бытовых условиях. Наиболее точные результаты дают электронные частотомеры.

Внешний вид электронного частотомера
Расчёт частоты тока
Для расчёта требуется знать период или временной отрезок, в течение которого значение переменного тока повторяется и образует одну полную волну. Между периодом и частотой переменного тока имеется зависимость, которую отражает следующая формула:

Определение частоты электротока
Если известно значение циклической частоты ɷ и амплитуда А, то по схожей зависимости можно вычислить силу тока I:

Определение силы электротока
Определение угловой частоты выполняется с помощью такого уравнения:

Формула угловой скорости
Переменный ток

Переме́нный ток, электрический ток, изменяющийся во времени по величине и/или направлению. В общем случае к переменному току относят различные виды импульсных, пульсирующих, периодических и квазипериодических токов. Если любые значения переменного тока повторяются через равные промежутки времени, то переменный ток называется периодическим. Периодом T T T переменного тока называется наименьший промежуток времени, в котором силы тока в моменты времени t t t и t + T t + T t + T равны: i ( t ) = i ( t + T ) i(t) = i(t + T) i ( t ) = i ( t + T ) . В технике под переменным током обычно подразумевают периодический (или близкий к периодическому) ток, в котором средние за период значения силы тока и напряжения равны нулю.
В том случае, когда переменный ток меняется по направлению, одно из направлений переменного тока принимают за положительное, а противоположное – за отрицательное. Соответственно, если направление переменного тока в некоторый момент времени совпадает с положительным направлением, то значение тока также считают положительным, а для противоположного направления тока – отрицательным. В простейшем случае мгновенное значение силы переменного тока изменяется во времени по гармоническому закону (гармонический, или синусоидальный, переменный ток):
i = I m s i n ( ω t + α ) i = I_msin( omega t+α) i = I m s in ( ω t + α ) ,
где I m I_m I m амплитуда тока, α alpha α – начальная фаза, ω = 2 π f ω = 2πf ω = 2 π f – круговая частота, f = 1 / T f = 1/T f = 1/ T – линейная частота. Гармонический ток возникает под действием синусоидального напряжения u той же частоты:
u = U m s i n ( ω t + β ) u = U_msin(ωt+β) u = U m s in ( ω t + β ) ,
где U m U_m U m – амплитуда напряжения, β beta β – начальная фаза.
Для характеристики переменного тока удобно использовать действующие (или эффективные) значения тока и напряжения, которые представляют собой среднеквадратичные (за период) значения силы тока и напряжения. Для синусоидальных токов действующие значения переменного тока и напряжения равны: I = I m 2 displaystyle I= frac < sqrt[]> I = 2
I m и U = U m 2 displaystyle U= frac < sqrt[]> U = 2
U m . Большая часть приборов, используемых для измерения периодических напряжений и токов, показывает действующие значения этих величин. Произведение действующих значений тока и напряжения определяет мощность, которая расходуется на выделение теплоты или на совершение механической работы в электрической цепи .
Важной характеристикой переменного тока является его частота f. В электроэнергетических системах Российской Федерации и большинства стран мира принята стандартная частота f f f = 50 Гц, в США f f f = 60 Гц. В технике связи применяются переменные токи высокой частоты (от 100 кГц до 30 ГГц). Для специальных целей в промышленности, медицине и других отраслях науки и техники используют переменный ток самых различных частот, а также импульсные токи .
В электротехнике (и частично в радиотехнике) обычно реализуются электрические цепи квазистационарных токов , при этом мгновенные значения переменного тока во всех участках цепи одинаковы. В многопроводных квазистационарных системах, предназначенных для передачи энергии, часто используют многофазные переменные токи – текущие по разным проводам токи с одинаковыми амплитудами, но разными фазами . Большинство цепей, содержащих сопротивления, ёмкости и индуктивности, работает в линейном режиме, когда справедлив принцип суперпозиции . При прохождении через такие цепи гармонические переменные токи не искажают своей формы, тогда как при наличии нелинейных элементов (например, сердечников в трансформаторах, нелинейных преобразователей, электронных ламп и т. п.) синусоидальные сигналы искажаются, обогащаясь высшими гармониками – сигналами на частотах, кратных основной частоте. Квазистационарные цепи с сосредоточенными параметрами могут быть составлены в виде определённой комбинации сопротивлений R R R , индуктивностей L L L и ёмкостей C C C . Если в электрической цепи протекает установившийся квазистационарный электрический ток, то напряжения на сопротивлении u R u_R u R , индуктивности u L u_L u L и ёмкости u C u_C u C определяются соотношениями:
u R = i R uR = iR u R = i R , u L = L d i d t displaystyle u_L=L frac u L = L d t d i , C d u C d t = i displaystyle C frac=i C d t d u C = i .
Для синусоидального тока i = I m sin ω t i = I_m sin omega t i = I m sin ω t соответствующие амплитудные значения напряжений на данных элементах равны:
U R m = R I m U_=RI_m U R m = R I m , U L m = ω L I m U_= omega LI_m U L m = ω L I m , U C m = I m ω C displaystyle U_= frac < omega C>U C m = ω C I m .
В нелинейных режимах величины R R R , L L L и C C C являются функциями протекающего тока i; в линейных режимах они либо постоянны, либо зависят в явном виде от времени (параметрические системы).
При расчёте электрических цепей гармонических переменных токов удобно использовать комплексные амплитуды напряжения и тока, а также комплексные сопротивления Z Z Z ( импеданс ), определяемые на резистивных, индуктивных и ёмкостных участках цепи соответственно как
Z R = R Z_R=R Z R = R , Z L = j ω L Z_L=j omega L Z L = jω L и Z C = 1 j ω C displaystyle Z_C= frac Z C = jω C 1 (здесь j j j – мнимая единица).
Тогда квазистационарная линейная цепь (многополюсник) может быть рассчитана по правилам Кирхгофа , т. е. в этом случае применимы методы расчётов цепей постоянного тока.
С ростом частоты, когда размер электрической цепи становится сравнимым с длиной электромагнитной волны λ = c / f lambda = c/f λ = c / f ( c c c – скорость света), квазистационарное приближение перестаёт быть справедливым, и для получения распределения переменного тока необходимо применять уравнения Максвелла . При этом протекающий по проводящей среде переменный ток распределяется по сечению не равномерно, а преимущественно в поверхностном слое. Иногда такие токи называют быстропеременными и оперируют не суммарными (интегральными) силами тока, а их объёмными плотностями. Плотность быстропеременных токов включает потенциальную и вихревую компоненты. Последняя ответственна за возбуждение вихревых электромагнитных полей. В открытых (неэкранированных) системах именно с вихревыми переменными токами связано излучение электромагнитной энергии, что используется, например, в излучателях (антеннах), где путём подбора распределений быстропеременных токов создаются требуемые угловые распределения полей излучения (диаграммы направленности).
Опубликовано 22 июня 2022 г. в 11:23 (GMT+3). Последнее обновление 22 июня 2022 г. в 11:23 (GMT+3). Связаться с редакцией
Период и частота переменного тока

Движение электронов в проводе сначала в одну сторону, а затем в другую называют одним колебанием переменного тока. За первым колебанием следует второе, затем третье и т. д. При колебаниях тока в проводе вокруг него происходит соответствующее колебание магнитного поля.
Время одного колебания называют периодом и обозначают буквой Т. Период выражают в секундах или в единицах, составляющих доли секунды. К ним относятся: тысячная доля секунды — миллисекунда (мс), равная 10 -3 с, миллионная доля секунды — микросекунда (мкс), равная 10 -6 с, и миллиардная доля секунды — наносекунда (нс), равная 10 -9 с.
Важной величиной, характеризующей переменный ток, является частота. Она представляет собой число колебаний или число периодов в секунду и обозначается буквой f или F. Единицей частоты служит герц, названный в честь немецкого ученого Г. Герца и обозначаемый сокращенно буквами Гц (или Hz). Если в одну секунду происходит одно полное колебание, то частота равна одному герцу. Когда в течение секунды совершается десять колебаний, то частота составляет 10 Гц. Частота и период являются обратными величинами:


При частоте 10 Гц период равен 0,1 с. А если период равен 0,01 с, то частота составляет 100 Гц
В электрической сети переменного тока частота равна 50 Гц. Ток пятьдесят раз в секунду идет в одну сторону и пятьдесят раз в обратную. Сто раз в секунду он достигает амплитудного значения и сто раз становится равным нулю, т. е. сто раз меняет свое направление при переходе через нулевое значение. Лампы, включенные в сеть, сто раз в секунду притухают и столько же раз вспыхивают ярче, но глаз этого не замечает, благодаря зрительной инерции, т. е. способности сохранять полученные впечатления около 0,1 с.
При расчетах с переменными токами пользуются также угловой частотой ω, она равна 2πf или 6,28f. Ее следует выражать не в герцах, а в радианах в секунду (радиан — угол в 2π раз меньший, чем 360 о ).

Переменные токи принято разделять по частоте. Токи с частотой меньше 10 000 Гц называют токами низкой частоты (токами НЧ). У этих токов частота соответствует частоте различных звуков человеческого голоса или музыкальных инструментов, и поэтому они иначе называются токами звуковой частоты (за исключением токов с частотой ниже 20 Гц, которые не соответствуют звуковым частотам). В радиотехнике токи НЧ имеют большое применение, особенно в радиотелефонной передаче.
Однако главную роль в радиосвязи выполняют переменные токи с частотой более 10000 Гц, называемые токами высокой частоты, или радиочастоты (токи ВЧ). Для измерения частоты этих токов применяют единицы: килогерц (кГц), равный тысяче герц, мегагерц (МГц), равный миллиону герц, и гигагерц (ГГц), равный миллиарду герц. Иначе килогерц, мегагерц и гигагерц обозначают kHz, MHz, GHz. Токи частотой в сотни мегагерц и выше называют токами сверхвысокой или ультравысокой частоты (СВЧ и УВЧ).
Радиостанции работают с помощью переменных токов ВЧ, имеющих частоту от сотен килогерц и выше. В современной радиотехнике для специальных целей применяются токи с частотой в миллиарды герц и имеются приборы, позволяющие точно измерять такие сверхвысокие частоты.
Величины, характеризующие переменный ток
В промышленных генераторах используют много пар магнитных полюсов. От их количества прямо пропорционально зависит значение частоты переменного тока. В различных государствах пользуются переменным током разной стандартной частоты: в Соединённых Штатах Америки — (60) Гц, в Российской Федерации — (50) Гц. Это значит, что происходит изменение направления электрического тока за (1) секунду (50) раз в каждую сторону.
Сила тока, получаемого с помощью такого генератора, изменяется с течением времени по гармоническому закону.

По графику силы тока видно, что она меняется от максимального ( амплитудного ) значения до нуля и обратно на протяжении одного периода.
При вычислении работы и мощности переменного тока необходимо учитывать гармоническую зависимость от времени значений силы тока (I(t)) и напряжения (U(t)), поэтому вводятся термины « мгновенная мощность (P(t))» и « средняя мощность (P)».
Для того чтобы формула средней мощности переменного тока (при наличии в электрическом контуре только сопротивления) не отличалась от формулы мощности постоянного тока ((P = UI)), вводятся термины « действующее значение силы тока » и « действующее значение напряжения ».
Как определяется
Существует два способа установить, чему равна частота и амплитуда переменного тока — применять специальные приборы либо воспользоваться результатами расчётов.
Измерение частоты
Для измерения частоты переменного тока используется принцип механического резонанса. Он является достаточно простым, хотя и не очень точным. Основывается на том факте, что для каждого физического объекта, обладающего упругими свойствами, существует определенное значение частоты, при которой он начинает вибрировать.
Примером подобного устройства является камертон. Если по нему ударить, он будет довольно продолжительное время вибрировать со звуком, зависящим от его длины. Чем длиннее камертон, тем ниже будет резонансная частота и наоборот.
Если представить себе ряд камертонов с постепенно увеличивающимися размерами, установленными на общем основании, то это основание станет вибрировать с частотой измеряемого напряжения или тока. Для этого устройство следует снабдить электромагнитом.
Измерения частоты тока выполняются с помощью набора «камертонов», в качестве которых используются полоски листового металла. Это устройство называется частотомером вибрирующего геркона.

Схема вибрационного частотомера
Используя частотомер, можно наглядно увидеть, как концы всех полосок встряхиваются в зависимости от того, как меняется величина переменного напряжения, приложенного к катушке. Тот из лепестков, который будет ближе всего к резонансной частоте переменного тока, станет вибрировать наиболее интенсивно.
Особой точностью вибрационные частотомеры не отличаются, зато характеризуются простотой своего изготовления. Их применяют в небольших электроремонтных мастерских, а также в быту с целью калибровки частоты вращения двигателя.
Хотя подобный прибор будет иметь малую точность, этого нельзя сказать о самом принципе измерения. Заменив механический резонатор на электрический, можно получить частотомер на основе катушки индуктивности и параллельно включённого конденсатора. Вместе они образуют колебательный контур.
Один или оба компонента этого контура могут быть регулируемыми. В цепь включается измерительный блок, который показывает максимальную амплитуду напряжения на конденсаторе и катушке. Ручки регулировки предварительно откалибровываются, чтобы иметь возможность выставлять резонансную частоту для любого варианта настройки. Частота считывается после настройки устройства на максимальное показание шкалы измерителя.

Схема электрического частотомера
Фактически частотомер реализует схему настраиваемого фильтра, после чего отсчёт показаний происходит как в мостовой схеме (она вначале балансируется для условного нулевого состояния, после чего выполняется отсчёт). До тех пор, пока катушка и/или конденсатор смогут перехватывать достаточное поле магнитного или электрического рассеивания от тестируемой цепи, устройство будет сохранять свою работоспособность.
Метод не требует прямого подключения к цепи, поэтому часто применяется в бытовых условиях. Наиболее точные результаты дают электронные частотомеры.

Внешний вид электронного частотомера
Расчёт частоты тока
Для расчёта требуется знать период или временной отрезок, в течение которого значение переменного тока повторяется и образует одну полную волну. Между периодом и частотой переменного тока имеется зависимость, которую отражает следующая формула:

Определение частоты электротока
Если известно значение циклической частоты ɷ и амплитуда А, то по схожей зависимости можно вычислить силу тока I:

Определение силы электротока
Определение угловой частоты выполняется с помощью такого уравнения:

Формула угловой скорости
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
p = ( I m a x cos . ω t ) 2 R
Вспомним из курса математики:
cos 2 . α = 1 + cos . 2 α 2 . .
p = I 2 m a x 2 . . R ( 1 + cos . 2 ω t ) = I 2 m a x R 2 . . + I 2 m a x R 2 . . cos . 2 ω t
График зависимости мгновенной мощности от времени:
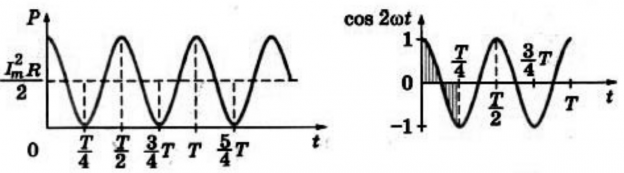
На протяжении первой четверти периода, когда cos . 2 ω t > 0 , мощность в любой момент времени больше величины I 2 m a x R 2 . . . На протяжении второй четверти периода, когда cos . 2 ω t < 0 , мощность в любой момент времени меньше этой величины. Среднее за период значение cos . 2 ω t = 0 , следовательно, средняя за период мощность равна I 2 m a x R 2 . . .
Средняя мощность − p равна:
− p = I 2 m a x R 2 . . = − i 2 R
Пример №2. Сила переменного тока в цепи меняется по закону i = I m a x cos . ω t . Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.
p = ( I m a x cos . ω t ) 2 R = 10 ( 1 · cos . ( 100 π · 1 ) 2 = 10 ( Д ж )
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
− i 2 = I 2 m a x 2 . .
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I = √ − i 2 = I m a x √ 2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
U = √ − u 2 = U m a x √ 2 . .
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
P = ( I m a x √ 2 . . ) 2 R = I 2 m a x 2 . . R = 2 2 2 . . · 5 = 10 ⎛ ⎝ Д ж ⎞ ⎠
Текст: Алиса Никитина, 7k
Задание EF22720
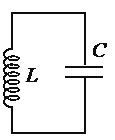
В идеальном колебательном контуре (см. рисунок) напряжение между обкладками конденсатора меняется по закону UC = U0cos ωt, где U0 = 5 В, ω = 1000π с – 1 . Определите период колебаний напряжения на конденсаторе.
Алгоритм решения




