Впервые позиционная система счисления возникла в древнем Вавилоне. В Индии система работает в виде позиционной десятичной нумерации с использованием нуля, у индусов данную систему чисел позаимствовала арабская нация, у них, в свою очередь, взяли европейцы. В Европе эту систему стали называть арабской.
Позиционная система счисления — значение всех цифр зависит от позиции (разряда) данной цифры в числе.
Примеры , стандартная десятичная система счисления – это позиционная система. Допустим, дано число 453 . Цифра 4 обозначает сотни и соответствует числу 400, 5 — кол-во десятков и соответствует значению 50 , а 3 — единицы и значению 3 . Легко заметить, что с увеличением разряда увеличивается значение. Таким образом, заданное число запишем в виде суммы 400+50+3=453.
Шестнадцатеричная система счисления.
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления. Основанием шестнадцатеричной системы счисления является число 16.
Записывая числа в восьмеричной системе счисления мы получаем довольно компактные выражения, однако в шестнадцатеричной системе мы получаем выражения более компактными.
Первыми десятью цифрами из шестнадцати шестнадцатеричных цифрах является стандартный интервал 0 — 9, последующие шесть цифр выражают при помощи первых букв латинского алфавита: A, B, C, D, E, F. Перевод из шестнадцатеричной системы в двоичную систему и в обратную сторону делают аналогично процессу для восьмеричной системы.
Для чего нужна шестнадцатеричная система
Итак, шестнадцатеричная система счисления, как следует из названия, имеет в своём основании число 16. Почему так? Дело в том, что единица информации в информатике – это бит. Восемь бит образуют байт. Также информационной среде существует такое понятие, как машинное слово – это минимальная единица данных, представляющая собой шестнадцать бит, то есть два байта. Считается, что машинное слово – это минимальная величина разрядности регистров процессора, при которой можно работать с ЭВМ.
Так вот, как мы знаем, компьютер работает на двоичном коде. Однако, если Вы когда-нибудь переводили числа из двоичной системы в десятичную, то замечали, что в ней бывает довольно много разрядов, особенно при переводе больших чисел, например, перевод числа 5132 в двоичной системе будет записано так:

Как можно увидеть, при переводе в двоичную систему этого числа у нас получилось аж 13 разрядов (с 0 до 12). Довольно муторно, а главное, занимает много места на письме и отнимает много времени для перевода.
Именно для этого придумали восьмеричную и шестнадцатеричную системы счисления, для этого придумали и байты. Эти системы помогают сократить затраты на перевод чисел и привести их к более приятному визуальному виду.
Если перевести то же число 5132 в восьмеричную систему счисления, то получится «более сокращённая версия» двоичного кода:
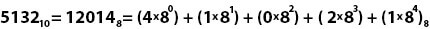
Как мы видим, количество символов сократилось, так как разрядность уменьшилась до 5 (с 0 до 4).
Как можно уже понять, шестнадцатеричная система ещё сильнее сокращает разрядность (с 0 до 3) и ещё сильнее сжимает на письме переведённое число:
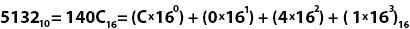
Человеку такой вид записи в любом случае удобнее, чем бесконечные нули и единицы.
Таким образом, шестнадцатеричная система используется довольно широко в современных информационных системах. Например, при помощи неё указываются коды цветовых схем, данная система используется для записи кодов ошибок, а также для программирования на языках низкого уровня типа Ассемблера, шестнадцатеричную систему зачастую используют для предоставления данных и адресов в малоразрядных ЭВМ.
Как перевести из десятичной системы в шестнадцатеричную
Выше мы уже немного затронули процесс перевода чисел. Теперь мы рассмотрим его подробнее и на примерах.
Но прежде чем начать, надо узнать одну очень важную особенность шестнадцатеричной системы.
Так как система имеет своим основанием число 16, то, следовательно, всего в этой системе имеется 16 цифр, но если первые десять цифр (0-9) вполне привычные для нас, то остальные имеют вид не совсем цифровой, но, тем не менее, являются цифрами, а именно значения A, B, C, D, E, F, которые соответствуют нашим привычным числам с 10 до 15. Все цифры шестнадцатеричной системы и их «аналоги» в десятичной записаны в таблице ниже.

Итак, допустим, у нас есть число 40 563 в десятичной системе счисления. Переведём его в шестнадцатеричную.
- Сначала мы просто делим наше исходное число 40 563 на 16 в столбик. В частном у нас получилось 2 535, если умножить это число на 16, то получится 40 560, а в остатке 3. Эту тройку мы выделяем.
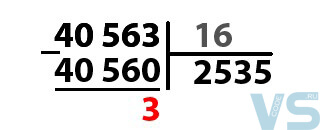
- Теперь мы делим 2 535, и тоже на 16, и тоже абсолютно таким же образом. Частное – 158, 16*158 = 2 528, а в остатке 7. Остаток так же, как и в тот раз, выделяем.
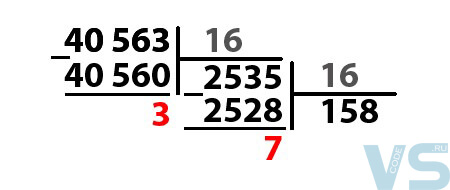
- Делим полученные частные до тех пор, пока они не станут меньше 16 , тогда деление заканчивается. Делим 158 на 16, и находим остаток от этого деления.
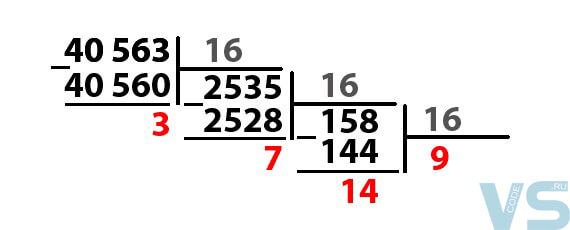
Остаток от деления – 14, а частное, полученное при делении 158 на 16 равно 9. Так как 9 меньше 16, то процесс вычислений закончен, а 9 также выделяется.
- Процесс преобразования десятичного числа в шестнадцатеричное почти окончен. Для того, чтобы получить его, надо всего лишь выписать выделенные числа справа налево (т.е. в данном случае от девятки к тройке), НО, как мы писали выше, у шестнадцатеричной системы свой особый «алфавит» с 10 по 15. И как раз один из наших «остатков» (число 14) вписывается в этот диапазон, поэтому надо посмотреть в таблице, либо просто самостоятельно посчитать, что в шестнадцатеричной системе 14 будет буквой Е.
Итого весь процесс преобразования приведён на следующем изображении:
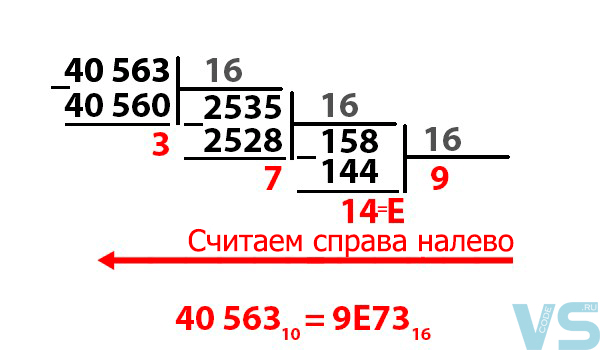
Таким образом мы научились переводить числа из десятичной системы в шестнадцатеричную. Теперь давайте попробуем сделать обратное преобразование, но уже с другим числом.
Перевод 16 –10
Для прямого перевода шестнадцатеричного числа в десятичную систему удобно пользоваться развернутой формой записи, когда число представляют в виде суммы, в которой слагаемые получаются путем умножения символа разряда (числа или числового эквивалента буквы) на 16 в степени соответствующего разряда.
Например, 1F4 = 1 * (16^2) + 15 * (16^1) + 4 * (16^0) = 256 + 240 + 4 = 500
Обратный перевод выполняется последовательным делением десятичного числа на 16 и взятия остатков от деления. Причем полученные остатки в диапазоне от 10 до 15 надо заменить соответствующей буквой.
Выполняя обратный перевод, следует помнить, что результирующее значение получают путем записи полученных от деления остатков в обратном порядке, начиная с последнего частного. Каждый остаток от деления должен получаться всегда меньше шестнадцати.
Например: 500 / 16 = 31 (остаток 4)
31 / 16 = 1 (остаток 15 заменяем на букву F)
Таким образом, получено шестнадцатеричное число 1F4.
Перевод 16 – 2
Для перевода шестнадцатеричного числа в десятичную систему каждую его цифру заменяют группой из четырех нулей и единиц, которую принято называть «тетрадой». Для перевода обычно пользуются таблицей соответствия шестнадцатеричных символов и двоичных тетрад.
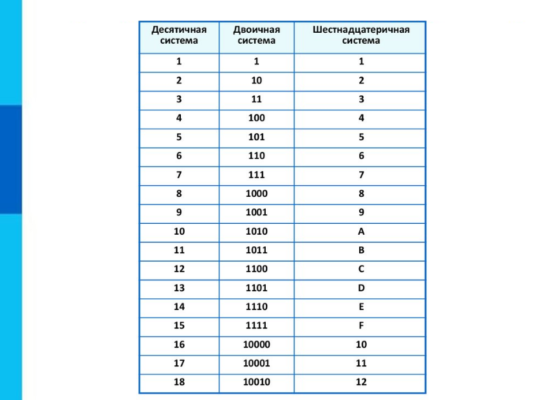
Например, 1F4 = (0001)(1111)(0100).
Число записанное в шестнадцатеричной системе счисления может состоять только из цифр

Уважаемые коллеги, мы рады предложить вам, разрабатываемый нами учебный курс по программированию ПЛК фирмы Beckhoff с применением среды автоматизации TwinCAT . Курс предназначен исключительно для самостоятельного изучения в ознакомительных целях. Перед любым применением изложенного материала в коммерческих целях просим связаться с нами. Текст из предложенных вам статей скопированный и размещенный в других источниках, должен содержать ссылку на наш сайт heaviside.ru . Вы можете связаться с нами по любым вопросам, в том числе создания для вас систем мониторинга и АСУ ТП.
Системы счисления
Уважаемые коллеги, эта статья будет полностью состоять из теории, мы рассмотрим системы счисления. При чтении этой статьи вы познакомитесь с двоичной и шестнадцатеричной системами счисления. Возможно, кому-то из читателей материал по системам счисления и переводу чисел из одной системы в другую может показаться сложным или скучным. Однако автор настоятельно рекомендует понять хотя бы их базовые принципы, так как в области программирования ПЛК, как и во многих других сферах программирования, они все еще достаточно актуальны и часто требуются на практике.
Бит, байт и размер данных
В прошлых статьях, когда мы рисовали схемы на языке LD, мы использовали тип данных BOOL. BOOL — это простейший тип данных, который может принимать всего два значения: и , они же FALSE и TRUE и содержит в себе количество информации, соответствующее одному биту. Бит — это наименьшее количество информации. Один бит равен количеству информации, получаемой в результате осуществления одного из двух равновероятных событий. Например, выпадение орла или решки при бросании монетки. Помимо бита для обозначения количества информации применяют понятие байта. В современных системах обычно имеют в виду, что байт состоит из восьми бит. При записи в качестве единицы измерения биты записываются как «бит», а байты как «Б», например, бит, Б. Как и для других единиц измерения, для записи количества информации перед единицей измерения используются десятичные приставки СИ . Кроме того, для битов и байтов используют двоичные приставки .
| Название | Обозначение | Степень |
| кило | К | |
| мега | М | |
| гига | Г | |
| терра | Т | |
| пета | П |
Например, Кбит = бит = КБ = Б.
| Название | Обозначение | Степень | Множитель |
| кибибайт | Ки (Ki) | ||
| мебибайт | Ми (Mi) | ||
| гибибайт | Ги (Gi) | ||
| тебибайт | Ти (Ti) | ||
| пебибайт | Пи (Pi) |
Например, Кибит = бит = КиБ = Б.
Иногда при написании десятичных приставок имеются в виду двоичные, то есть при записи КБ имеется в виду Б. Такое использование приставок формально хоть и не является корректным, но очень часто встречается на практике.
Также стоит отметить, что иногда под словом байт подразумевается размер регистров процессора, то есть количество бит, которое процессор может обрабатывать за раз. Размер регистров процессора называется разрядность (или битность) процессора. Из контекста всегда можно понять, что имеется в виду: бит или один разряд процессора. Современные процессоры, работающие под управлением Windows, имеют разрядность в или бита.
Системы счисления
Наверное, всем известно, что компьютеры оперируют данными в виде единиц и нолей. Такая система счисления называется двоичной позиционной. Система счисления — это способ записи цифр. Двоичная система наиболее удобна для применения в электронных схемах. Нулю соответствует отсутствие напряжения, единице — его наличие, или наоборот, в электронике достаточно часто единице соответствует отсутствие напряжение, нулю его наличие.
История знает попытки создания компьютеров на основе других систем счисления. Например, советский компьютер Сетунь , который использовал троичную систему счисления, или американский Mark I с десятичной системой. Но какого-либо серьезного распространения компьютеры, основанные на системах счисления, отличных от двоичной, не получили.

Системы счисления делятся на позиционные, непозиционные и смешанные:
![]()
- Позиционные системы счисления — системы счисления, в которых значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда). Например, рассмотрим число , — означает количество сотен, — количество десятков, — количество единиц. Так, арабская система счисления, которой все мы пользуемся в повседневной жизни, является десятичной позиционной системой. Обратим внимание на слово «десятичная». В данном примере оно связано с основанием системы счисления, а именно количеством знаков, используемых для записи числа в той или иной системе. В десятичной системе для записи используются цифры . Основанием является число .
- Смешанные системы счисления, — системы счисления, в которых числа, заданные в некоторой системе счисления с основанием P, изображаются с помощью цифр другой системы счисления с основанием Q, где Q
- Непозиционные системы счисления — системы счисления, в которых величина, обозначаемая цифрой, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания. Примерами непозиционных счисления являются римская , египетская и система остаточных классов .
![]()
Далее в этой статье речь пойдет только о позиционных системах счисления. Как говорилось выше, в компьютерах применяют двоичную позиционную систему счисления. Для начала давайте разберемся, что такое число и чем оно отличается от цифры. Число используется для счета и выражает количество. Цифры — это набор знаков для записи чисел. В арабской системе счисления цифрами являются знаки , в двоичной — и . Каждая цифра в записи числа, называется разрядом. В информатике разряд числа считается справа налево, начиная с нуля. При записи в десятичной системе числа цифра является нулевым разрядом, цифра — первым, цифра — вторым разрядом.
Двоичная система счисления имеет основание , то есть в ней используется всего две цифры: и . Числа ноль и один в десятичной и в двоичной системах выглядят абсолютно одинаково и записываются как и соответственно. А вот цифры в двоичной системе нет, поэтому приходится добавить еще один разряд, число два в двоичной системе будет записываться как . Что бы записать число три, надо добавить к двойке единицу, выглядит это так . Для записи числа четыре снова надо добавить еще один разряд, в результате получаем . Пять записывается как и так далее.
| Десятичная | Двоичная |
Шестнадцатеричная система счисления
Двоичная система весьма неудобна для восприятия человеком. Например, число , записанное в двоичной системе, будет выглядеть как , а число соответствует записи . Для более удобного восприятия человеком числа часто представляют в шестнадцатеричной системе счисления. Переводить числа из одной системы счисления в другую мы научимся позже в этой статье.
Как и в других позиционных системах счисления, принцип записи чисел в шестнадцатеричной системе схож с рассмотренной выше двоичной системой и всем знакомой с детства десятичной. Разница лишь в том, что следующей после цифры идет (десятичная ), а новый разряд добавляется после цифры (десятичная ). В шестнадцатеричной системе счисления для записи используются следующие цифры:
| Десятичная цифра | Шестнадцатеричная цифра |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
Применение именно шестнадцатеричной системы обусловлено легкостью перевода данных в нее из двоичной и обратно, а также наглядностью записи, которая обусловлена тем, что один разряд шестнадцатеричного числа эквивалентен четырем разрядам двоичного числа. То есть байт двоичного кода записывается ровно двумя цифрами шестнадцатеричного числа. Число , в двоичной системе выглядит как , а в шестнадцатеричной . Причем четыре старших разряда двоичного числа записываются шестнадцатиричной , а четыре младших разряда двоичного числа записываются шестнадцатеричным числом .
В этой статье мы используем сразу три системы счисления. Не всегда можно понять, какая система счисления применяется для записи числа, если это не указанно явно. Например, цифры могут означать три в двоичной системе, одиннадцать в десятичной и семнадцать в шестнадцатеричной. Во избежание путаницы, в математике принято указывать основание применяемой системы счисления в виде индекса после записанного числа. К примеру, запись означает, что применена двоичная система. Если индекс не указан предполагается что применена десятичная система.
При написании программ достаточно часто возникает необходимость указать в какой системе счисления записано число. В языках МЭК это делается с помощью префиксов добавляемых к числу.
| Префикс | Система счисления |
| # | двоичная |
| # | восьмеричная |
| отсутствует | десятичная |
| # | шестнадцатеричная |
То есть двоичное число в TwinCAT записывается как # .
Восьмеричная система хоть и поддерживается в TwinCAT, но в настоящее время почти не используется. Изложенного выше материала должно быть достаточно для ее понимания.
Перевод чисел из двоичной системы в десятичную и обратно
В сети материала со строгим изложением теоретических выкладок по переводу чисел из одной системы счисления в другую достаточно много. Здесь мы рассмотрим лишь один из удобных на практике способов перевода чисел между различными системами, несильно вдаваясь в теорию этого процесса.
В позиционных системах счисления любое число можно представить в виде где: — основание системы счисления. — числа, равные цифре, стоящей в разряде k.
Выглядит сложно, но на практике довольно просто, число можно представить в виде:
![]()
![]()
Кстати, именно из-за такой формы записи разряды чисел считают, начиная с нуля, а не с единицы.
Число (десятичное ) можно представить в виде:
![]()
![]()
Вспомнив, что можно продолжить выражение.
![]()
![]()
Можно заметить, что достаточно запомнить, какое десятичное значение соответствует каждому двоичному разряду и просуммировать их при переводе.
| Номер разряда | Двоичное значение | Десятичное значение |
Для перевода из двоичной системы в десятичную и обратно приведенную выше таблицу следует выучить наизусть.
Давайте решим несколько примеров для закрепления:
![]()
![]()
Перевод из десятичной системы в двоичную производится следующим образом: из десятичного числа вычитается ближайшее меньшее число, из только что выученной нами наизусть таблицы, и записывается соответствующие ему двоичное, после чего действие повторяется с остатком. Когда остатка не осталось, суммируем все записанные двоичные числа.
Приведем пример с числом :
- Ближайшее меньшее к число из таблицы . Записываем . Остатком будет .
- Повторяем действие. Ближайшее к число из таблицы — . Пишем . Остаток .
- Ближайшее к число . Записываем . Остаток .
- Числу соответствует число , его и записываем.
- В результате предыдущих действий мы получили числа , , , . После сложения получится .
Как видите, перевод из двоичной системы счисления в десятичную и обратно не составляет большой сложности.
Перевод чисел из двоичной системы в шестнадцатеричную и обратно
В целом порядок перевода в десятичную и в шестнадцатиричную систему схожи. Главное отличие в том, таблица перевода будет повторяться каждые четыре строчки, так как 16=24. Таким образом, выучив всего четыре строчки, вы сможете переводить числа любого размера.
| Номер разряда | Двоичное значение | Шестнадцатеричное значение |
В таблице намеренно показано больше чем четыре строчки, что бы читатели могли увидеть как именно повторяются значения.
Повторим некоторые примеры, которые мы приводили для десятичной системы:
![]()
![]()
Перевод из шестнадцатеричной системы в двоичную производится аналогично переводу из десятичной в двоичную, но проще, так как производится группами по 4 бита. Напомним, из шестнадцатеричного числа вычитается ближайшее меньшее число из таблицы перевода между двоичными и шестнадцатеричными числами, после чего действие повторяется с остатком. После того, как остатка не будет, суммируем все записанные двоичные числа.
Приведем пример с числом (десятичное ):
- Ближайшее меньшее к число из таблицы , записываем . Остатком будет .
- Повторяем действие, ближайшее к число из таблицы — , записываем . Остаток .
- Ближайшее к число — , записываем . Остаток .
- Числу соответствует число , его и записываем.
- В результате предыдущих действий мы получили числа , , , . После сложения получится .
Еще один простой способ перевода чисел между системами счисления – это использование стандартного калькулятора в Windows (предварительно необходимо переключить в режим «Программист»).
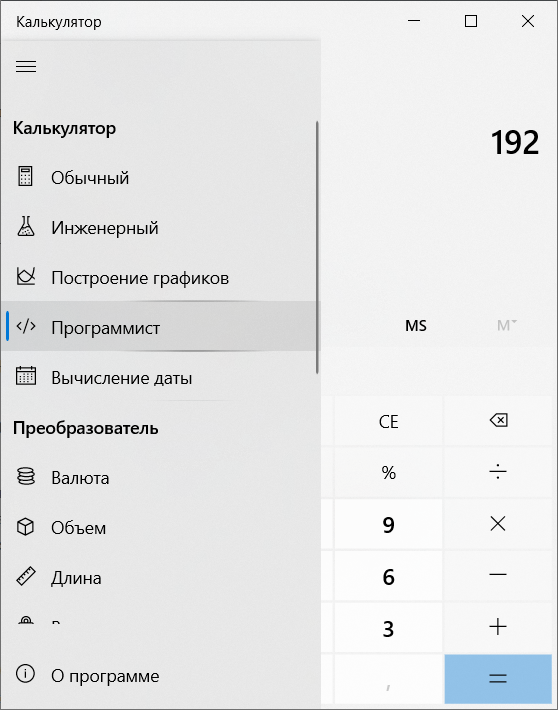
Хотя такой способ может показаться соблазнительным, но стоит научиться переводить в уме числа хотя бы до одного байта (как читатель теперь уже может убедиться самостоятельно, в один байт можно записать числа в диапазоне от до ). С приобретением практики это станет не сложнее умножения двузначных чисел.
Подсчёт в шестнадцатеричной системе счисления
Это возвращает нас к счёту в нашей системе счисления с основанием 16: шестнадцатеричной. Теперь мы знаем шаги, которым нужно следовать, и можем сосчитать (пропустим подсчёт от нуля до девяти): 0… пропуск до… 9… A… B… C… D… E… F… 10… 11…. Теперь мы понимаем, что 10 в шестнадцатеричной системе счисления, как и в восьмеричной, имеет другое значение, чем то, что мы можем подумать (исходя из нашей привычки пользоваться десятичной системой счисления), поскольку мы ведём счёт в шестнадцатеричной системе счисления, которая соответствует основанию равному 16, а не десятичной системе счисления, в которой основание равно 10. Число 10 в шестнадцатеричном формате на самом деле равно 16 в десятичном!
Примечательно, что шестнадцатеричный формат, именно потому, что он состоит из 16 оснований, позволяет нам хранить весь байт в двух символах! Мы не можем сделать это с десятичным числом, поскольку двоичное значение 1111 1111 (т.е. 1111111 для компьютера) равно 255 в десятичном формате. Однако в шестнадцатеричном формате оно может быть представлено как FF, который в десятичном виде равен 255. Также обратите внимание, что полбайта, 4 бита, можно сохранить в одном шестнадцатеричном символе.
Подведение итогов
Мы надеемся, что вам понравилось это введение в шестнадцатеричную, нашу 16-символьную или 16-базовую числовую систему, а также в двоичную систему счисления с двумя базовыми числами и восьмеричную систему счисления с основанием числа 8. Мы также узнали, как мы ведём ежедневный счёт в десятичной системе счисления, в нашей очень знакомой десятичной системе счисления используются числа от 0 до 9.
Мы также увидели, что символы, которые мы используем для представления двоичных, восьмеричных, шестнадцатеричных и даже десятичных значений, — это всего лишь символы, которые человечество выбрало для представления этих различных систем счисления. Мы могли бы легко выбрать другие представления для других числовых систем, но повторное использование тех же чисел кажется знакомым и имеет некоторый смысл, особенно в случае двоичной системы «напряжение» и «отсутствие напряжение», представлены нулём и единицей.
Перевод шестнадцатеричного числа в двоичное
Итак, сколько же предметов обозначает число 10?
Как видно из таблицы 1, все будет зависит от того, какое основание выбрано для числа. Это может быть и 10 предметов, и 2, и 16.
Для информации
В некоторых случаях внизу числа указывают индекс, который и отображает основание. Если такой индекс присутствует, то при записи 1010 речь идет о десяти предметах (число из системы с основанием 10).
Запись 102 обозначает 2 предмета, поскольку является двоичным числом 10 «один-ноль» в системе с основанием 2.
В случае же индекса 16 запись 1016 обозначает шестнадцать предметов, так как основание системы счисления равно 16.
В качестве примера переведем шестнадцатеричное число С316 в двоичное число.
Рисунок 1 показывает, как каждый символ шестнадцатеричного числа переводится в его четырехсимвольный двоичный эквивалент (воспользуемся таблицей 1).
Шестнадцатеричный символ С (старший разряд) соответствует четырехразрядному двоичному числу 1100, а шестнадцатеричный символ 316 (младший разряд) — двоичному числу 0011. Объединяя эти две двоичные группы, получаем, что С316 = 11000011 .
| Шестнадцатеричное число | C | 316 |
| ↓ | ↓ | ↓ |
| Двоичное число | 1100 | 0011 |
Перевод двоичного числа в шестнадцатеричное
Выполним теперь противоположную операцию и переведем двоичное число 11101010 в соответствующее ему шестнадцетиричное. Эта операция изображена на рисунке 2.
Двоичное число разбивается на группы по 4 разряда и вместо них подставляется соответствующий шестнадцетиричный эквивалент (таблица 1 в помощь).
В результате получаем 111010102 = ЕА16
| Двоичное число | 1110 | 10102 |
| ↓ | ↓ | ↓ |
| Шестнадцатеричное число | E | A16 |
Шестнадцатеричная система счисления
Основание шестнадцатеричной системы — число 16 (записанное здесь в десятичной системе счисления).
В этой системе шестнадцать базисных чисел: ноль, один, два, три, четыре, . девять, десять, одиннадцать, . пятнадцать (также записанных здесь в десятичной системе), и шестнадцать цифр, первые десять из которых заимствованы из десятичного цифрового алфавита: 0, 1, 2, 3, 9, а недостающие шесть — из латин
ского буквенного: А, В, С, Э, Е и Е.
При поразрядном сложении 16 единиц младшего разряда объединяются в одну единицу старшего, при поразрядном вычитании «заемная» единица старшего разряда рассматривается как 16 единиц младшего:

Для вычисления десятичного значения шестнадцатеричного числа (перевод из шестнадцатеричной в десятичную систему) применяется описанная ранее общая формула (все числа и вычисления — в десятичной системе).
Пример перевода шестнадцатеричного числа 1234,СЕ16 в десятичную систему счисления:

Для обратного перевода из десятичной в шестнадцатеричную систему надо представить исходное десятичное число в виде суммы произведений базисных чисел шестнадцатеричной системы счисления на целочисленные степени числа 16 и затем записать эти числа в соответствующих позициях.

следовательно, в первой позиции восьмеричного числа будет записана цифра 3, в нулевой позиции — цифра А, а в «минус первой» позиции — цифра 2. В результате получим: 58,12510 = ЗА,216.
Для перевода из двоичной системы счисления в шестнадцатеричную можно использовать уже знакомую формулу, однако при этом следует иметь в виду, что нумеровать позиции и выполнять все вычисления следует в шестнадцатеричной системе счисления:

Табл. 3.2 иллюстрирует представление чисел в позиционных системах счисления: десятичной, двоичной, восьмеричной и шестнадцатеричной.
Анализ числовых данных, приведенных в табл. 3.2, позволяет сделать ряд полезных замечаний:
- 1) чем больше основание системы счисления, тем компактнее в ней запись числа;
- 2) десятичные числа, представляющие целые степени двойки, записываются в двоичной, восьмеричной и шестнадцатеричной системах круглыми числами, что является следствием того, что основания восьмеричной и шестнадцатеричной систем счисления сами являются целыми степенями двойки;
- 3) двоичная запись десятичных чисел, представляющих целые степени двойки, всегда содержит единицу в старшем бите и нули во всех остальных битах, количество которых равно степени двойки соответствующего десятичного числа;
- 4) для двоичной записи любого одноразрядного (базисного) восьмеричного числа потребуется не более трех битов (8 = 2 3 );
- 5) для двоичной записи любого одноразрядного (базисного) десятичного или шестнадцатеричного числа потребуется не более четырех битов (2 3 4 , 16 = 2 4 ).
Представление чисел в позиционных системах счисления 1
Восьмеричная
Шестнадцатеричная




