Каждый день вас окружает множество волн. В этой статье вы узнаете, что это такое и какими свойствами они обладают.
В качестве концепции вы можете представить волну как форму с последовательными восходящими и нисходящими частями. К этой категории относится, например, волна воды.
Однако эти части, поднимающиеся и опускающиеся вверх и вниз, не являются случайными по форме и расположению, а следуют очень определенной схеме. Этот паттерн показывает, как частицы среды, в которой распространяется волна, колеблются вверх и вниз. Частицы «возмущаются» волной определенным образом.
Определение: под волной можно представить возмущение в среде, которое движется с фиксированной формой и постоянной скоростью.
На рисунке 1 показано, например, как такое возмущение в виде холма движется по веревке слева направо. Во время движения частицы веревки поднимаются вверх от переднего конца возмущения и тянутся вниз от заднего конца.

От света, который вам нужен, чтобы видеть, до звука, который вам нужен, чтобы слышать, до интернет-сигнала, который вам нужен для работы в Интернете, — все это волны. Как видите, волны — неотъемлемая часть жизни человека.
Виды волн
В этом подразделе мы рассмотрим различные виды волн и то, к какой области теоретической физики они относятся.
Поперечные и продольные волны
Например, в волне воды, которая движется слева направо, отдельные частицы воды колеблются вверх и вниз. Поэтому движение частиц перпендикулярно движению волны. Эти типы волн называются поперечными и могут быть поляризованными.
Звуковые волны (также называемые для краткости звуком), которые позволяют вам слышать, являются примером продольных волн. В продольных волнах частицы вовлеченной среды колеблются в направлении движения волны. Поэтому движение частиц параллельно движению волн.

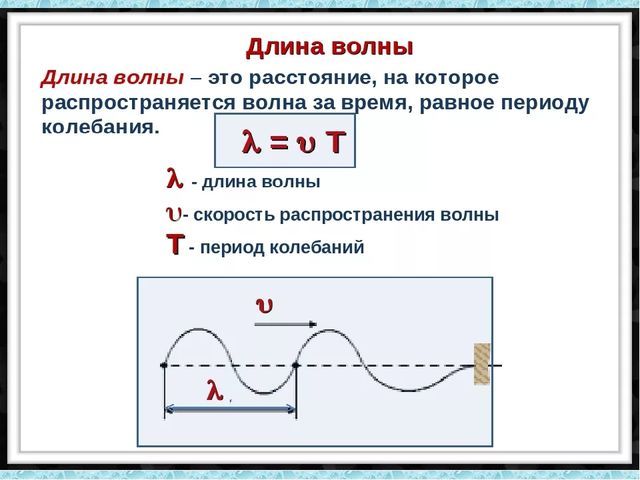
Длина волны. Связь длины волны со скоростью её распространения и периодом (частотой)
Скорость волны зависит от строения вещества и взаимодействия между её молекулами (атомами). Поэтому в различных средах скорость одной и той же волны будет отличаться.
Помимо скорости, важной характеристикой волны является длина волны.
Длина волны — расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Рассмотрим процесс передачи колебаний от точки к точке при распространении поперечной волны.
Используется модель, в которой частицы среды заменяют шариками. Для удобства их можно пронумеровать (рис. (1)).
Длина и скорость волны
Частицы среды связаны между собой межмолекулярными силами взаимодействия, поэтому волна передаётся от одной частицы к другой.
![]()
Рис. (1). Модель упругой среды для демонстрации колебаний
Отклоним первый шарик от положения равновесия. Силы притяжения передадут движение второму, третьему шарику. Каждый элемент вещества (молекула, атом) повторит движение первой частицы с запаздыванием, которые называют сдвигом фазы. Это запаздывание зависит от расстояния, на котором находится рассматриваемый шарик по отношению к первому шарику.
Предположим, что первый шарик достиг максимального смещения от положения равновесия (рис. (2)). В этот момент четвёртый шарик только начнет движение, следовательно, он отстаёт от первого на (1/4) колебания.

Рис. (2). Изображение максимального смещения от положения равновесия первого шарика
В момент времени, когда смещение четвертого шарика будет наибольшим (рис. (3)), седьмой шарик будет отставать от него на (1/4) колебания. А если рассмотреть отставание седьмого шарика от первого, то оно составляет (1/2) колебания.

Рис. (3). Изображение максимального смещения от положения равновесия четвёртого шарика
Между седьмым и четвёртым шариком, а также седьмым и десятым (1/4) часть колебания (рис. (4)).

Рис. (4). Изображение максимального смещения от положения равновесия седьмого шарика
Первый и тринадцатый шарик совершают одно колебание, то есть двигаются в одной фазе (рис. (5)). Это значит, что между ними все шарики с первого по двенадцатый проходят полный колебательный процесс или составляют одну волну.
Ваш браузер не поддерживается
Интернет-сервис Студворк построен на передовых, современных технологиях и не может гарантировать полную поддержку текущего браузера.

Установить новый браузер
- Google Chrome

Скачать
Яндекс Браузер

Скачать
Opera

Скачать
Firefox

Скачать
Microsoft Edge
Нажимая на эту кнопку, вы соглашаетесь с тем, что сайт в вашем браузере может отображаться некорректно. Связаться с техподдержкой
Работаем по будням с 8.00 до 18.00 по МСК
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ) , единицы измерения – с.

Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ) , единицы времени – с -1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:

Период и частота колебаний – взаимно обратные величины:

Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ) , единицы измерения – рад/с.

Параметры волны
Фаза, период и частота
Для распространяющейся волны можно ввести параметр, который называется фазой. Фаза – это одинаковое состояние среды распространения. Для поверхности воды фаза – это величина отклонения от спокойного состояния (от нулевого уровня). Точки волны, находящиеся в одинаковом состоянии, будут находиться в одинаковых фазах. Если записывать в таблицу время, проходящее между одинаковыми фазами какой-то точки, то можно заметить, что это время будет кратно некоторому минимальному значению. Это значение, минимальное время, за которое волна оказывается в одной и той же фазе, называется периодом колебаний $T$ волны. Число периодов за одну секунду называется частотой волны $nu$ (для обозначения используется греческая буква «ню»):
Фазу можно сопоставить с углом на координатной плоскости. Полная волна соответствует углу $2pi$, все фазы повторяются с этим периодом точно так же, как повторяется значение круговых функций (синуса, косинуса и других).
Одному значению отклонения от нулевого значения соответствуют две фазы – одна в момент возрастания, другая – в момент спадания волны (исключение – самый «пик» или самое «дно» волны). Это разные фазы, путать их не следует.
Скорость распространения и длина волны
Поскольку волна распространяется не мгновенно, то, отметив одинаковую фазу волны (движущийся гребень), можно определить скорость этого распространения $v$ относительно неподвижных предметов (например, относительно берега, в случае, когда волна распространяется вдоль него). Для вычисления используется обычная формула скорости – отношение пройденного расстояния к прошедшему времени. Кроме того, можно ввести понятие «длина волны».
Расстояние, которое проходит волна за один период колебания, называется длиной волны, для обозначения используется греческая буква $lambda$ (лямбда). Формула длины волны:
Если известна частота колебаний, для расчета удобнее пользоваться другой формулой (она вытекает из определения частоты):
Слышимый звук представляет из себя колебания плотности воздуха. Распространяется он в нормальных условиях со скоростью, имеющей значения порядка 300-350м/с, и имеет длину волны от ~15мм (самые высокие частоты) до ~15м (самые низкие частоты)
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Длина волны. Период и частота колебаний. Связь скорости с длиной волны и частота колебаний. Принцип радиосвязи. Модуляция. Детектирование
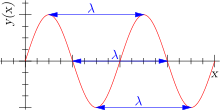
График волны функции (например, физической величины) y, распространяющейся вдоль оси Оx, построенный в фиксированный момент времени (t = const). Длина волны λ может быть измерена как расстояние между парой соседних максимумов y (x) либо минимумов, либо как удвоенное расстояние между соседними точками, в которых y = 0.
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. [1][2]
Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π [3]
Длину волны можно также определить:
- как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на 2π;
- как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
- как пространственный период волнового процесса.
Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Тогда длина волны — это расстояние между двумя соседними гребнями волны, измеренное в радиальном направлении. Длина волны — одна из основных характеристик волны наряду с частотой, амплитудой, начальной фазой, направлением распространения и поляризацией. Для обозначения длины волны принято использовать греческую букву , размерность длины волны — метр.
Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (наиболее низкочастотной, фундаментальной) гармоники спектра.
В случае если известны длина волны и скорость распространения колебаний, частоту вычислите следующим образом:
F=v/λ, где F — частота (Гц), v — скорость распространения колебаний в среде (м/с), λ — длина волны (м).
Если известна частота, период найти можно и в том случае, если скорость распространения колебаний неизвестна. Формула для вычисления периода по частоте выглядит следующим образом:
T=1/F, где T — период колебаний (с), F — частота (Гц).
Из сказанного выше следует, что найти частоту, зная период, можно также без информации о скорости распространения колебаний. Способ ее нахождения такой же:
F=1/T, где F — частота (Гц), T — период колебаний (с).
Для того чтобы узнать циклическую частоту колебаний, вначале вычислите их обычную частоту любым из указанных выше способов. Затем умножьте ее на 2π:
ω=2πF, где ω — циклическая частота (радиан в секунду), F — обычная частота (Гц)
Отсюда следует, что для вычисления обычной частоты при наличии информации о циклической следует воспользоваться обратной формулой:
F=ω/(2π), где F — обычная частота (Гц), ω — циклическая частота (радиан в секунду).
При решении задач на нахождение периода и частоты колебаний, а также длины волны используйте следующие физические и математические константы:
— скорость света в вакууме: c=299792458 м/с (некоторые исследователи, в частности, креационисты, считают, что в прошлом данная физическая константа могла иметь другую величину);
— скорость звука в воздухе при атмосферном давлении и нуле градусов по Цельсию: Fзв=331 м/с;
— число «пи» (до пятидесятого знака): π=3,14159265358979323846264338327950288419716939937510 (безразмерная величина
длина волны есть частное от деления скорости на частоту.
Если волна пробегает в секунду 100 метров, при этом ее частота 50 Гц (50 колебаний в секунду), то в 100 метрах уложится 50 колебаний, и значит 1 колебание занимает 2 метра.
Радиосвязь- электросвязь посредством радиоволн. Для осуществления радиосвязи в пункте, из которого ведётся передача сообщений (радиопередача), размещают радиопередающее устройство, содержащее радиопередатчик и передающую антенну, а в пункте, в котором ведётся приём сообщений (радиоприём), — радиоприёмное устройство, содержащее приёмную антенну и радиоприёмник. Генерируемые в передатчике гармонические колебания с несущей частотой, принадлежащей какому-либо диапазону радиочастот, подвергаются модуляции в соответствии с передаваемым сообщением. Модулированные радиочастотные колебания представляют собой радиосигнал. От передатчика радиосигнал поступает в передающую антенну, посредством которой в окружающем антенну пространстве возбуждаются соответственно модулированные электромагнитные волны. Распространяясь, радиоволны достигают приёмной антенны и возбуждают в ней электрические колебания, которые поступают далее в радиоприёмник. Принятый т. о. радиосигнал очень слаб, т. к. в приёмную антенну попадает лишь ничтожная часть излученной энергии. Поэтому радиосигнал в радиоприёмнике поступает в электронный усилитель, после чего он подвергается демодуляции, или детектированию; в результате выделяется сигнал, аналогичный сигналу, которым были модулированы колебания с несущей частотой в радиопередатчике. Далее этот сигнал (обычно дополнительно усиленный) преобразуется при помощи соответствующего воспроизводящего устройства в сообщение, адекватное исходному.
В месте приёма на радиосигнал могут накладываться электромагнитные колебания от посторонних источников радиоизлучений, способные помешать правильному воспроизведению сообщения и называемые поэтому помехами радиоприёму. Неблагоприятное влияние на качество радиосвязи могут оказывать также изменение во времени затухания радиоволн на пути распространения от передающей антенны к приёмной и распространение радиоволн одновременно по двум или нескольким траекториям различной протяжённости; в последнем случае электромагнитное поле в месте приёма представляет собой сумму взаимно смещенных во времени радиоволн, интерференция которых также вызывает искажения радиосигнала. Поэтому и эти явления относят к категории помех радиоприёму. Их влияние на приём радиосигналов особенно велико при связи на больших расстояниях. Широкое распространение радиосвязи и использование радиоволн в радиолокации, радионавигации и др. областях техники потребовали обеспечения одновременного функционирования без недопустимых взаимных помех различных систем и средств, использующих радиоволны, — обеспечения их электромагнитной совместимости.
Распространение радиоволн в открытом пространстве делает возможным в принципе приём радиосигналов, передаваемых по линиям радиосвязи, лицами, для которых они не предназначены (радиоперехват, радиоподслушивание); в этом — недостаток радиосвязи по сравнению с электросвязью по кабелям, радиоволноводам и др. закрытым линиям. Тайна телефонных переговоров и телеграфных сообщений, предусматриваемая соответствующими правилами международными соглашениями, обеспечивается в необходимых случаях применением автоматических средств засекречивания радиосигналов (кодирование и др.).
Модуляция — превращение электрического тока в радио сигнал, а детектирование — обнаружение или пелингация сигнала в пространстве. Может Вы имели в виду «декодирование» — это перевод радио волны высокой чистоты в электрический сигнал.
46)Природа света. Длина волны света. Энергия кванта.
См 20.04.15 и 26.05.15
47)Законы отражения и преломления света. Полное отражение света.
48)Интерференция света. Условия максимума и минимума интерференционной картины.
Смотреть в тетрадь за 18.05.15
49)Дифракция света. Дифракционная решётка. Условия максимума дифракционной решётки.
Смотреть в тетрадь за 25.05.15
50)Дисперсия света. Разложение белого цвета призмов. Спектры.
Диспе́рсия све́та (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Экспериментально открыта Ньютоном около 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее.
Белый свет разлагается призмой на спектральные цвета (спектр): красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. Это распределение «главных» цветов было предложено Ньютоном по аналогии со звуковой гаммой. Между
отдельными цветами происходят непрерывные переходы тонов. Красный свет отклоняется меньше всего, фиолетовый имеет наибольший угол отклонения. При помощи цилиндрической линзы можно снова соединить спектральные цвета в белый свет Следовательно, белый цвет является смесью множества цветных лучей спектра.
Если ввести в сходящийся пучок лучей позади цилиндрической линзы вторую (тонкую призму, то она отклонит часть лучей и на экране появится окрашенное изображение щели, например светло-голубое; неотклонённые лучи дадут второе изображение щели (оранжевое). Эти два пучка лучей дадут совместно белый цвет. Такого рода цвета: красный и зеленый, оранжевый и светло-голубой, желтый и синий называют дополнительными цветами.
Замечание. Желтый и синий спектральные цвета дают совместно белый; но соединение желтой и синей красок дает зеленый цвет. В последнем случае речь идет об отраженном свете. Желтая краска отражает главным образом оранжевый, желтый и зеленый. Синяя отражает, наоборот, зеленый и синий. В смеси преобладает отраженный зеленый цвет.
Одинаковые призмы из разных сортов стекла дают спектры различной ширины. Комбинируя призмы с различными преломляющими углами, можно уменьшить отклонение и одновременно увеличить ширину спектра (спектроскоп прямого зрения). Комбинируя призмы из флинтгласа и кронгласа с различными преломляющими углами, можно, наоборот, устранить разложение в спектр и сохранить отклонение: ахроматические призмы.
Спектр — совокупность значений, которые может принимать физическая величина, характеризующая некоторую систему или некоторый процесс
Оптический спектр — спектр излучения или спектр поглощения оптического излучения. Различают:
— линейчатые оптические спектры;
— полосатые оптические спектры, состоящие из групп близких спектральных линий;
— сплошные оптические спектры, соответствующие излучению или поглощению электромагнитного излучения в широком диапазоне длин волн.
Сплошной спектр,
непрерывный спектр, спектр электромагнитного излучения, распределение энергии в котором характеризуется непрерывной функцией частоты излучения [j(n)] или длины его волны [f(l), см. Спектры оптические]. Для С. с. функция (j(n) [или f(l)] слабо изменяется в достаточно широком диапазоне n (или l), в отличие от линейчатых и полосатых спектров, когда j(n) имеет при дискретных значениях частоты n = n1, n2, n3. выраженные максимумы, очень узкие для спектральных линий и более широкие для спектральных полос. В оптической области при разложении света спектральными приборами С. с. получается в виде непрерывной полосы (при визуальном наблюдении или фоторегистрации; см. рис.) или плавной кривой (при фотоэлектрической регистрации). С. с. наблюдаются как в испускании, так и в поглощении. Примером С. с., охватывающего весь диапазон частот и характеризуемого вполне определённым спектральным распределением энергии, является спектр равновесного излучения. Он характеризуется Планка законом излучения.
В некоторых случаях возможны наложения линейчатого спектра на сплошной.
Например, в спектрах Солнца и звёзд на С. с. испускания могут накладываться как дискретный спектр поглощения (фраунгоферовы линии), так и дискретный спектр испускания (в частности, спектральные линии испускания атома водорода).
mydocx.ru — 2015-2024 year. (0.005 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав — Пожаловаться на публикацию
Частота период длина волны
Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной .
Механические волны бывают разных видов. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной . Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне.
Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной . Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн.
Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.
Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.
Распространение поперечного волнового импульса по натянутому резиновому жгуту
Распространение продольного волнового импульса по упругому стержню
Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами . В реальных средах эти свойства распределены по всему объему. Так, например, любой малый элемент твердого тела обладает массой и упругостью. В простейшей одномерной модели твердое тело можно представить как совокупность шариков и пружинок (рис. 2.6.3).
Простейшая одномерная модель твердого тела
В этой модели инертные и упругие свойства разделены. Шарики обладают массой , а пружинки – жесткостью . С помощью такой простой модели можно описать распространение продольных и поперечных волн в твердом теле. В продольных волнах шарики испытывают смещения вдоль цепочки, а пружинки растягиваются или сжимаются. Такая деформация называется деформацией растяжения или сжатия (см. §1.12). В жидкостях или газах деформация такого рода сопровождается уплотнением или разрежением .
Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
Если в одномерной модели твердого тела один или несколько шариков сместить в направлении, перпендикулярном цепочке, то возникнет деформация сдвига . Деформированные при таком смещении пружины будут стремиться возвратить смещенные частицы в положение равновесия. При этом на ближайшие несмещенные частицы будут действовать упругие силы, стремящиеся отклонить их от положения равновесия. В результате вдоль цепочки побежит поперечная волна.
В жидкостях и газах упругая деформация сдвига не возникает. Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появится. Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. То же относится к газообразной среде. Следовательно, поперечные волны не могут существовать в жидкой или газообразной средах .
Значительный интерес для практики представляют простые гармонические или синусоидальные волны . Они характеризуются амплитудой колебания частиц, частотой и длиной волны . Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью .
Смещение частиц среды из положения равновесия в синусоидальной волне зависит от координаты на оси , вдоль которой распространяется волна, и от времени по закону:
где – так называемое волновое число , – круговая частота.
На рис. 2.6.4 изображены «моментальные фотографии» поперечной волны в два момента времени: и . За время волна переместилась вдоль оси на расстояние . Такие волны принято называть бегущими (в отличие от стоячих волн, см. далее).
«Моментальные фотографии» бегущей синусоидальной волны в момент времени и
Длиной волны называют расстояние между двумя соседними точками на оси , колеблющимися в одинаковых фазах. Расстояние, равное длине волны , волна пробегает за период , следовательно, , где – скорость распространения волны.
Для любой выбранной точки на графике волнового процесса (например, для точки на рис. 2.6.4) с течением времени изменяется координата этой точки, а значение выражения не изменяется. Через промежуток времени точка переместится по оси на некоторое расстояние . Следовательно:
Таким образом, бегущая синусоидальная волна обладает двойной периодичностью – во времени и пространстве. Временной период равен периоду колебаний частиц среды, пространственный период равен длине волны . Волновое число является пространственным аналогом круговой частоты
Обратим внимание на то, что уравнение
описывает синусоидальную волну, распространяющуюся в направлении, противоположном направлению оси , со скоростью
В бегущей синусоидальной волне каждая частица среды совершает гармонические колебания с некоторой частотой . Поэтому, как и в случае простого колебательного процесса, средняя потенциальная энергия, запасенная в некотором объеме среды, равна средней кинетической энергии в том же объеме и пропорциональна квадрату амплитуды колебаний.
Отсюда следует, что при распространении бегущей волны возникает поток энергии, пропорциональный скорости волны и квадрату ее амплитуды.
Бегущие волны распространяются в средах с определенными скоростями, зависящими от типа волны, а также от инертных и упругих свойств среды.
Скорость поперечных волн в натянутой струне или резиновом жгуте зависит от погонной массы (т. е. массы единицы длины) и силы натяжения :
Скорость распространения продольных волн в безграничной среде определяется плотностью среды (т. е. массой единицы объема) и модулем всестороннего сжатия , который равен коэффициенту пропорциональности между изменением давления и относительным изменением объема , взятому с обратным знаком:
Выражение для скорости распространения продольных волн в безграничных средах имеет вид
Например, при температуре скорость распространения продольных волн в воде , в различных сортах стали .
При распространении продольных волн в упругих стержнях в формулу для скорости волн вместо модуля всестороннего сжатия входит модуль Юнга (см. §1.12):
Для стали отличие от невелико, для других материалов оно может составлять и даже больше.
Модель. Продольные и поперечные волны
Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения ( суперпозиции ) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.
Если волны, бегущие по струне во встречных направлениях, имеют синусоидальную форму, то при определенных условиях они могут образовать стоячую волну .
Пусть струна длины закреплена так, что один из ее концов находится в точке , а другой – в точке (рис. 2.6.5). В струне создано натяжение .
Образование стоячей волны в струне, закрепленной на обоих концах
По струне одновременно распространяются в противоположных направлениях две волны одной и той же частоты:
- – волна, бегущая справа налево;
- – волна, бегущая слева направо.
В точке (один из закрепленных концов струны) падающая волна в результате отражения порождает волну . При отражении от неподвижно закрепленного конца отраженная волна оказывается в противофазе с падающей. Согласно принципу суперпозиции , который является экспериментальным фактом, колебания, вызванные встречными волнами в каждой точке струны, складываются. Таким образом, результирующее колебание в каждой точке равно сумме колебаний, вызванных волнами 1 и 2 в отдельности. Следовательно,
Это и есть стоячая волна . В стоячей волне существуют неподвижные точки, которые называются узлами . Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями .
Оба неподвижных конца струны должны быть узлами. Приведенная выше формула удовлетворяет этому условию на левом конце (). Для выполнения этого условия и на правом конце (), необходимо чтобы , где – любое целое число. Это означает, что стоячая волна в струне возникает не всегда, а только в том случае, если длина струны равняется целому числу длин полуволн:
Набору значений длин волн соответствует набор возможных частот :
где – скорость распространения поперечных волн по струне. Каждая из частот и связанный с ней тип колебания струны называется нормальной модой . Наименьшая частота называется основной частотой , все остальные () называются гармониками . На рис. 2.6.5 изображена нормальная мода для .
В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не транспортируется в другие части струны. В каждом таком отрезке происходит периодическое (дважды за период ) превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Но в отличие от груза на пружине или маятника, у которых имеется единственная собственная частота струна обладает бесконечным числом собственных (резонансных) частот . На рис. 2.6.6 изображены несколько типов стоячих волн в струне, закрепленной на обоих концах.
Первые пять нормальных мод колебаний струны, закрепленной на обоих концах
В соответствии с принципом суперпозиции стоячие волны различных типов (т. е. с разными значениями ) могут одновременно присутствовать в колебаниях струны.




